1) Параметричні рівняння кривої в скалярній формі
Введемо в просторі прямокутну декартову систему координат. Нехай кожній точці 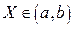 відповідає число t. Цій точці на
відповідає число t. Цій точці на 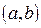 відповідає точка Р в просторі,
відповідає точка Р в просторі, 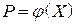 . Тоді кожному
. Тоді кожному 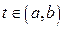 відповідає точка Р,а їй відповідають три просторові координати
відповідає точка Р,а їй відповідають три просторові координати 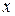 ,
, 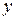 ,
, 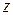 – функції від t:
– функції від t:
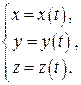 (1)
(1)
Рівняння (1) називаються параметричними рівняннями кривої 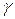 (в скалярній формі).
(в скалярній формі).
Окремі криві, які однозначно проектуються на деякий відрізок осі ОХ, можна задати особливо просто: 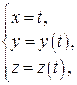 або
або 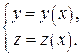 .
.
2) Параметричне рівняння кривої у векторній формі
При певному виборі декартової системи координат у просторі трійка функцій (1) однозначно визначає вектор-функцію
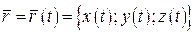 . (2)
. (2)
Рівняння (2) називається параметричним рівнянням кривої у векторній формі. Крива визначається як годограф вектор-функції  .
.
Параметричне задання кривої називається параметризацією.
Параметризація називається природною, якщо за параметр t прийнято довжину дуги s, причому 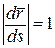 .
.
Крива називається регулярною класу 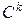 ( (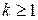 ), якщо існує така її параметризація ), якщо існує така її параметризація 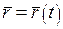 , що , що 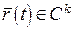 і і 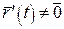 . Регулярну криву класу . Регулярну криву класу 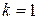 називають гладкою кривою. Якщо називають гладкою кривою. Якщо 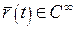 , то криву називають аналітичною. , то криву називають аналітичною. |
Зауваження. Вимога існує в означенні регулярної кривої істотна.
|
|
|
Приклад. Розглянемо криву на площині: 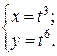
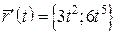 ,
, 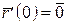 при
при 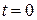 .
.
Але це не означає, що крива не регулярна. Може статися, що існує краща параметризація цієї кривої.
Справді, візьмемо іншу параметризацію: 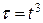 .
.
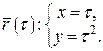
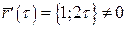 для будь-якого
для будь-якого 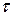 .
.
Отже, крива регулярна.
Задача. Скласти параметричне рівняння гвинтової лінії – траєкторії руху точки, яка обертається навколо прямої з постійною кутовою швидкістю 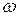 і одночасно переміщується в напрямі осі обертання зі сталою швидкістю
і одночасно переміщується в напрямі осі обертання зі сталою швидкістю 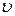 .
.
Розв’язання. Приймемо вісь обертання за Oz і будемо вважати, що початкове положення рухомої точки М0 знаходиться на осі Ox.
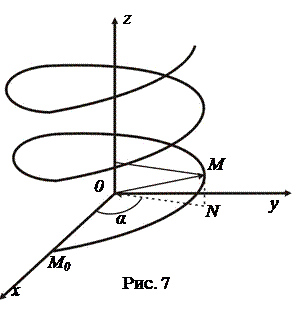 В довільний момент часу відстань точки М від осі обертання стала, отже М рухається по прямому круговому циліндру (рис.7).
В довільний момент часу відстань точки М від осі обертання стала, отже М рухається по прямому круговому циліндру (рис.7).
Нехай радіус циліндра а. Якщо t – час, то для кожної точки 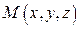 :
: 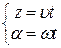 . Отже:
. Отже: 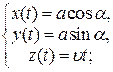 або
або 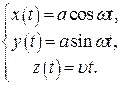

Відповідь: 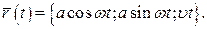
3) Неявно задана просторова крива (як перетин двох поверхонь):
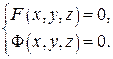 (3)
(3)
Застосовуючи теореми про неявні функції, можна показати, що рівняння (3) визначають регулярну елементарну криву в деякому околі її точки 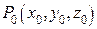 , якщо функції
, якщо функції 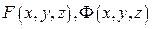 неперервні разом зі своїми частинними похідними в околі цієї точки і ранг матриці
неперервні разом зі своїми частинними похідними в околі цієї точки і ранг матриці 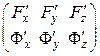 в цій точці дорівнює 2.
в цій точці дорівнює 2.
 2015-07-14
2015-07-14 856
856








