| Дотичною прямою до кривої в її даній точці називається граничне положення січної, яка проходить через дану точку та іншу точку кривої, яка необмежено наближається вздовж кривої до даної точки. |
В диференціальній геометрії використовується ще одне означення 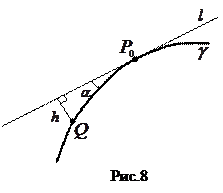 дотичної до кривої, еквівалентне наведеному вище (рис.8).
дотичної до кривої, еквівалентне наведеному вище (рис.8).
Нехай  – дана крива,
– дана крива,  ; l – пряма,
; l – пряма,  .
.
Візьмемо точку 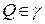 і позначимо її відстані: d – відстань Q від
і позначимо її відстані: d – відстань Q від 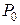 (
(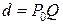 ), h – відстань Q від l.
), h – відстань Q від l.
Якщо 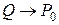 і
і 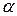 – кут між прямими l і
– кут між прямими l і 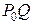 , то
, то 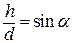 – показник співпадання січної
– показник співпадання січної 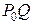 з l.
з l.
Граничне положення січної 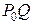 при
при 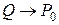 є дотичною до
є дотичною до 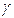 в точці
в точці 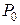 , при цьому
, при цьому 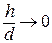 .
.
Пряма l називається дотичною до кривої 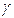 в точці в точці 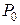 , якщо , якщо 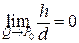 . . |
Теорема 5.Гладка крива, задана рівнянням 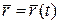 , , 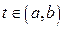 , у кожній своїй точці , у кожній своїй точці 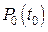 має єдину дотичну, яка паралельна вектору має єдину дотичну, яка паралельна вектору 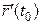 . . |
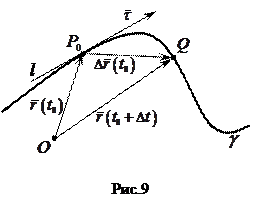 □ 1) Єдиність дотичної. Припустимо, що крива
□ 1) Єдиність дотичної. Припустимо, що крива 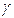 в точці
в точці 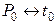 має дотичну l.
має дотичну l.
Нехай 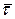 – одиничний вектор дотичної в точці
– одиничний вектор дотичної в точці 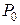 , точкам
, точкам 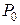 і Q кривої відповідають значення
і Q кривої відповідають значення 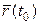 і
і 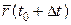 :
:
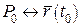 ,
, 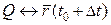 .
.
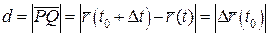 .
.
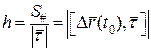 , де
, де 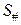 – площа паралелограма, побудованого на векторах
– площа паралелограма, побудованого на векторах 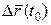 і
і 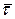 .
.
За означенням дотичної: 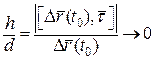 . (5)
. (5)
Потрібно перейти до границі при 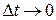 . Але у виразі для
. Але у виразі для 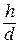 немає
немає 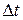 . Поділимо чисельник і знаменник на
. Поділимо чисельник і знаменник на 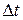 :
: 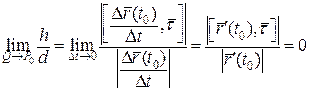 .
.
Звідси 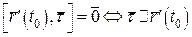 , оскільки
, оскільки 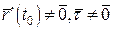 .
.
Таким чином, якщо дотична l існує, то вона має напрям вектора 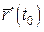 . Точка
. Точка 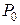 і вектор
і вектор 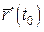 визначають єдину дотичну.
визначають єдину дотичну.
2) Існування дотичної. Дотична визначається точкою 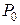 і напрямним вектором. З попередніх записів видно, що таким вектором може бути одиничний вектор, колінеарний вектору
і напрямним вектором. З попередніх записів видно, що таким вектором може бути одиничний вектор, колінеарний вектору 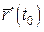 . Справді, розглянемо вектор
. Справді, розглянемо вектор 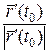 і запишемо
і запишемо 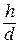 для прямої з таким напрямним вектором:
для прямої з таким напрямним вектором:
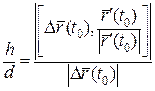 ;
; 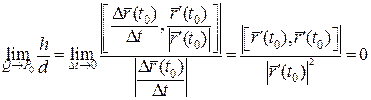 .
.
Це і означає, що пряма, яка визначається точкою 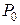 і напрямом
і напрямом 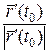 , є дотичною. ■
, є дотичною. ■
Зауваження. Тепер зрозумілий зміст обмеження 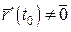 в означенні регулярної кривої. Це обмеження еквівалентне вимозі існування дотичної до кривої (напрям нульового вектора невизначений).
в означенні регулярної кривої. Це обмеження еквівалентне вимозі існування дотичної до кривої (напрям нульового вектора невизначений).
Знайдемо рівняння дотичної прямої для різних способів задання регулярної просторової кривої в точці 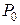 .
.
а) Крива задана параметричним рівнянням у векторній формі: 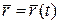 (рис. 10).
(рис. 10).
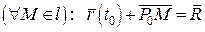
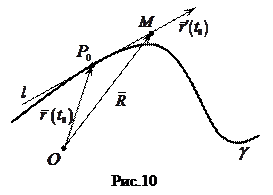 ,
,
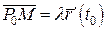 ,
, 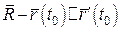 ,
,
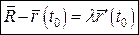 (6)
(6)
б) Крива задана параметричними рівняннями в скалярній формі 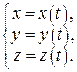
Позначимо координати точок  і M:
і M: 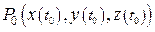 ,
, 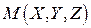 та скористаємось пропорційністю відповідних координат колінеарних векторів:
та скористаємось пропорційністю відповідних координат колінеарних векторів:
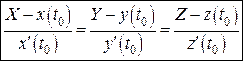 (
( )
)
в) Криву задано як перетин двох поверхонь: 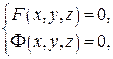
де функції 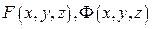 неперервні разом з їх частинними похідними в деякому околі точки
неперервні разом з їх частинними похідними в деякому околі точки 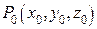 .
.
Припустимо, що в точці 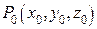 кривої
кривої 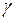 ранг матриці
ранг матриці 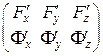 дорівнює 2. Це умова того, що в точці
дорівнює 2. Це умова того, що в точці 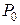 існує окіл, усі точки якого утворюють регулярну елементарну криву.
існує окіл, усі точки якого утворюють регулярну елементарну криву.
Нехай 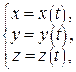 – регулярна параметризація цієї ж кривої в околі точки
– регулярна параметризація цієї ж кривої в околі точки 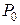 .
.
Підставивши ці функції в ліві частини рівнянь 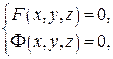 одержимо тотожності
одержимо тотожності 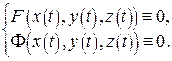
Продиференціюємо ці рівності по t, застосовуючи правило диференціювання складеної функції від трьох змінних:
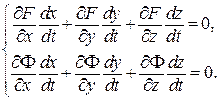
Ліві частини рівностей містять дві групи величин:
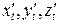 – похідні від координат в точці
– похідні від координат в точці 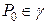 ;
;
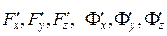 – частинні похідні від функцій, які визначають поверхні і обчислюються в точці
– частинні похідні від функцій, які визначають поверхні і обчислюються в точці 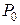 .
.
Складемо матрицю з елементів другої групи: 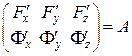 .
.
Оскільки її ранг дорівнює 2, то розв’язки однорідної системи можна подати через відношення визначників 2го порядку, складених з елементів матриці А:
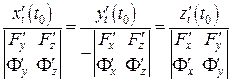 .
.
Підставимо в рівняння (6') замість 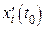 ,
, 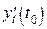 ,
, 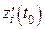 величини, їм пропорційні:
величини, їм пропорційні:
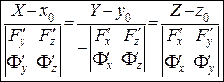 . (6")
. (6")
Задача. Знайти рівняння дотичної в точці (a,0,0) до гвинтової лінії 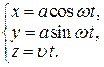
Розв’язання. Даній точці відповідає значення t=0.
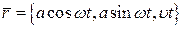 ;
; 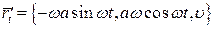 ;
; 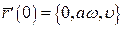 .
.
У відповідності з (6') запишемо рівняння дотичної: 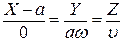 .
.
Відповідь: 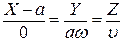 .
.
 2015-07-14
2015-07-14 1281
1281








