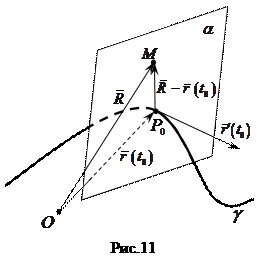
| Нормаллю кривої в даній її точці називається пряма, яка проходить через цю точку і перпендикулярна до дотичної, проведеної до кривої у цій точці. |
Просторова крива має нескінченну множину нормалей. Усі вони лежать в одній площині, яка називається нормальною площиною.
| Нормальною площиною кривої в даній її точці називається площина, яка проходить через дану точку і перпендикулярна до дотичної, проведеної до кривої у цій точці. |
 Нехай
Нехай 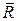 – радіус-вектор довільної точки M нормальної площини
– радіус-вектор довільної точки M нормальної площини 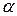 в точці
в точці 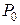 .
.
Тоді вектор 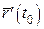 є нормальним вектором площини
є нормальним вектором площини 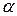 :
:
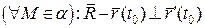 .
.
Відповідно до способу задання кривої маємо такі рівняння нормальної площини в точці 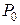 :
:
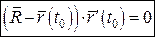 ; (7)
; (7)
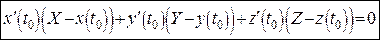 ; (7')
; (7')
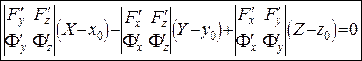 . (7")
. (7")
Задача. Скласти рівняння дотичної прямої та нормальної площини до кривої 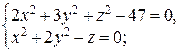 в точці
в точці 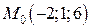 .
.
Розв’язання.
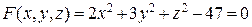 – рівняння еліпсоїда;
– рівняння еліпсоїда;
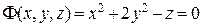 – рівняння параболоїда.
– рівняння параболоїда.
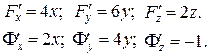
При 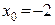 ;
; 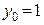 ;
; 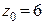 маємо:
маємо: 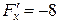 ;
; 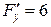 ;
; 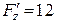 ;
;
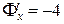 ;
; 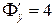 ;
; 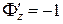 .
.
Отже: 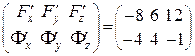 .
.
Рівняння дотичної прямої:
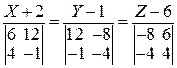 ;
; 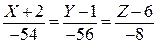 ;
; 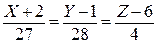 .
.
Рівняння нормальної площини:
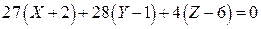 ;
; 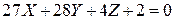 .
.
Відповідь: 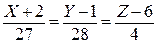 ;
;
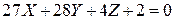 .
.
 2015-07-14
2015-07-14 722
722








