САМОСТОЯТЕЛЬНАЯ РАБОТА № 2.
Геометрический и механический смысл производной.
Цель работы: обобщить и систематизировать знания, умения и навыки по теме геометрический и физический смысл производной.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Геометрический смысл производной
Если функция дифференцируема в точке 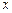 , то график этой функции имеет в соответствующей точке касательную, причем угловой коэффициент касательной равен значению производной в рассматриваемой точке. Угловой коэффициент касательной, проведенной к графику функции
, то график этой функции имеет в соответствующей точке касательную, причем угловой коэффициент касательной равен значению производной в рассматриваемой точке. Угловой коэффициент касательной, проведенной к графику функции 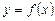 в точке,
в точке, 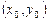 , равен значению производной функции при
, равен значению производной функции при 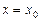 , т.е.
, т.е. 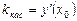 . Уравнение этой касательной имеет вид:
. Уравнение этой касательной имеет вид: 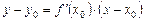 , где
, где 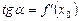 .
.
Алгоритм составления уравнения касательной к графику функции 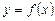
1. Обозначить буквой 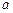 абсциссу точки касания.
абсциссу точки касания.
2. Найти 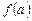 .
.
3. Найти 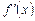 и
и 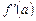 .
.
4. Подставить найденные числа 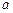 ,
, 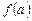 ,
, 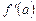 в общее уравнение касательной
в общее уравнение касательной 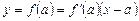 .
.
Вычленяют типа задач: 1) задачи на касательную, заданную точкой, через которую она проходит;
2) задачи на касательную, заданную ее угловым коэффициентом.
В первом типе задач были выделены две ключевые задачи:
- касательная проходит через точку, лежащую на кривой (задача 1);
- касательная проходит через точку, не лежащую на кривой (задача 2).
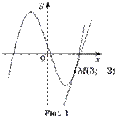 Задача 1. Составьте уравнение касательной к графику функции
Задача 1. Составьте уравнение касательной к графику функции 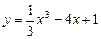 в точке
в точке 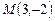 .
.
Решение. Точка 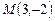 является точкой касания, так как
является точкой касания, так как 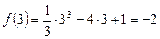 (рис.1)
(рис.1)
1. 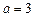 – абсцисса точки касания.
– абсцисса точки касания.
2. 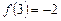 .
.
3. 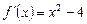 ,
, 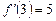 .
.
4. 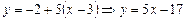 – уравнение касательной.
– уравнение касательной.
Задача 2. Напишите уравнения всех касательных к графику функции 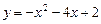 , проходящих через точку
, проходящих через точку 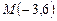 .
.
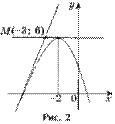 Решение. Точка
Решение. Точка 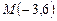 не является точкой касания, так как
не является точкой касания, так как 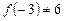 (рис. 2).
(рис. 2).
1. 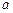 – абсцисса точки касания.
– абсцисса точки касания.
2. 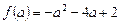 .
.
3. 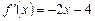 ,
, 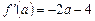 .
.
4. 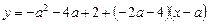 – уравнение касательной.
– уравнение касательной.
Касательная проходит через точку 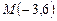 , следовательно, ее координаты удовлетворяют уравнению касательной.
, следовательно, ее координаты удовлетворяют уравнению касательной.
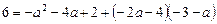
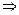
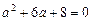
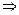
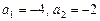 .
.
Если 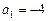 , то уравнение касательной имеет вид
, то уравнение касательной имеет вид 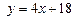 .
.
Если 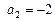 , то уравнение касательной имеет вид
, то уравнение касательной имеет вид 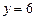 .
.
Во втором типе ключевыми задачами будут следующие:
- касательная параллельна некоторой прямой (задача 3);
- касательная проходит под некоторым углом к данной прямой (задача 4).
Задача 3. Напишите уравнения всех касательных к графику функции 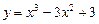 , параллельных прямой
, параллельных прямой 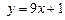 .
.
Решение.
1. 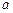 – абсцисса точки касания.
– абсцисса точки касания.
2. 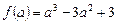 .
.
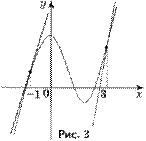 3.
3. 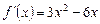 ,
, 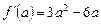 . Но, с другой стороны,
. Но, с другой стороны, 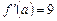 (условие параллельности). Значит, надо решить уравнение
(условие параллельности). Значит, надо решить уравнение 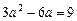 . Его корни
. Его корни 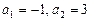 (рис. 3).
(рис. 3).
4. 1) Если 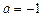 ; 2)
; 2) 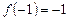 ; 3)
; 3) 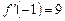 ; 4)
; 4) 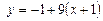 ;
;
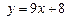 – уравнение касательной;
– уравнение касательной;
1) Если 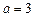 ; 2) 2)
; 2) 2) 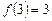 ; 3)
; 3) 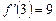 ; 4)
; 4) 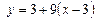 ;
;
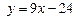 – уравнение касательной;
– уравнение касательной;
Задача 4. Напишите уравнение касательной к графику функции 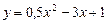 ,
, 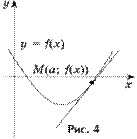 проходящей под углом
проходящей под углом 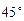 к прямой
к прямой 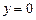 (рис. 4).
(рис. 4).
Решение. Из условия 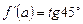 найдем
найдем 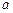 :
: 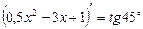
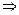
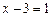
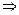
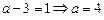 .
.
1. 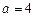 – абсцисса точки касания.
– абсцисса точки касания.
2. 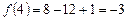 .
.
3. 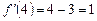 .
.
4. 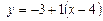 .
.
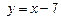 – уравнение касательной.
– уравнение касательной.
Решение любой другой задачи сводится к решению одной или нескольких ключевых задач. Рассмотрим в качестве примера следующие три задачи.
1. Напишите уравнения касательных к параболе 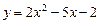 , если касательные пересекаются под прямым углом и одна из них касается параболы в точке с абсциссой
, если касательные пересекаются под прямым углом и одна из них касается параболы в точке с абсциссой 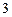 (рис. 5).
(рис. 5).
Решение. Поскольку дана абсцисса точки касания, то первая часть решения сводится к ключевой задаче 1.
1. 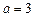 – абсцисса точки касания одной из сторон прямого угла.
– абсцисса точки касания одной из сторон прямого угла.
2. 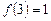 .
.
3. 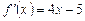 ,
, 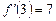 .
.
4. 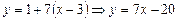 – уравнение первой касательной.
– уравнение первой касательной.
Пусть 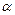 – угол наклона первой касательной. Так как касательные перпендикулярны, то
– угол наклона первой касательной. Так как касательные перпендикулярны, то 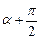 – угол наклона второй касательной. Из уравнения
– угол наклона второй касательной. Из уравнения 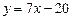 первой касательной имеем
первой касательной имеем 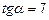 . Найдем
. Найдем 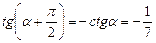 . Это значит, что угловой коэффициент второй касательной равен
. Это значит, что угловой коэффициент второй касательной равен 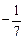 .
.
Дальнейшее решение сводится к ключевой задаче 3.
Пусть 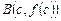 есть точка касания второй прямой, тогда
есть точка касания второй прямой, тогда 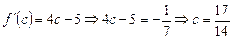 .
.
1. 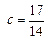 – абсцисса второй точки касания.
– абсцисса второй точки касания.
2. 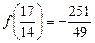 .
.
3. 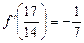 .
.
4. 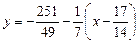
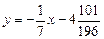 – уравнение второй касательной.
– уравнение второй касательной.
Примечание. Угловой коэффициент касательной может быть найден проще, если учащимся известно соотношение коэффициентов перпендикулярных прямых 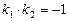 .
.
2. Напишите уравнения всех общих касательных к графикам функций 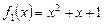 и
и 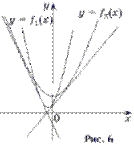
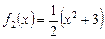 .
.
Решение. Задача сводится к отысканию абсцисс точек касания общих касательных, то есть к решению ключевой задачи 1 в общем виде, составлению системы уравнений и последующему ее решению (рис. 6).
1. Пусть 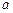 – абсцисса точки касания, лежащей на графике функции
– абсцисса точки касания, лежащей на графике функции 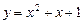
2. 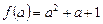 .
.
3. 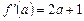 .
.
4. 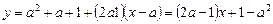 – уравнение касательной.
– уравнение касательной.
1. Пусть 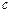 – абсцисса точки касания, лежащей на графике функции
– абсцисса точки касания, лежащей на графике функции 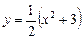
2. 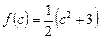 .
.
3. 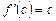 .
.
4. 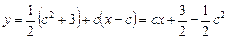
Так как касательные общие, то
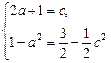
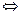
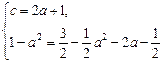
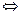
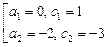
Итак, 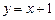 и
и 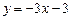 – общие касательные.
– общие касательные.
3. Задача, обратная к задаче 1, на нахождение функции по семейству ее касательных.
При каких 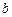 и
и 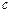 прямые
прямые 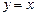 и
и 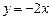 являются касательными к графику функции
являются касательными к графику функции 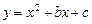 ?
?
Решение. Пусть 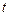 – абсцисса точки касания прямой
– абсцисса точки касания прямой 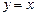 с параболой
с параболой 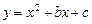 ;
; 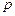 – абсцисса точки касания прямой
– абсцисса точки касания прямой 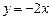 с параболой
с параболой 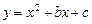 . Тогда уравнение касательной
. Тогда уравнение касательной 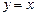 примет вид
примет вид 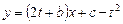 , а уравнение касательной
, а уравнение касательной 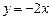 примет вид
примет вид 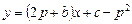 . Составим и решим систему уравнений
. Составим и решим систему уравнений
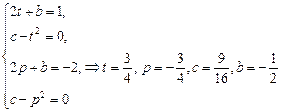
Ответ: 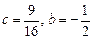 .
.
Физический смысл первой и второй производной
Необходимость изучения мгновенной скорости изменения функции возникает во многих случаях. Например, скорость химической реакции, скорость испарения жидкости, скорость изменения длины стержня при изменении температуры и т.д.
Если функция 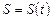 описывает закон прямолинейного движения материальной точки, то первая производная пути
описывает закон прямолинейного движения материальной точки, то первая производная пути 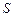 по времени
по времени 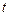 равна скорости движения, а вторая производная равна ускорению
равна скорости движения, а вторая производная равна ускорению 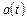 движения материальной точки в данный момент времени
движения материальной точки в данный момент времени 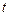 .
.
Пример 1. Точка движется по прямой по закону 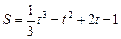 (
(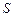 - метрах,
- метрах, 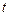 − в секундах). Найти скорость и ускорение в конце третьей секунды.
− в секундах). Найти скорость и ускорение в конце третьей секунды.
Решение. 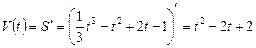 , тогда
, тогда 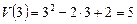 .
.
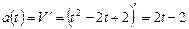 , тогда
, тогда 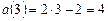 .
.
Ответ: 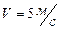 ,
, 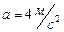 .
.
 2015-07-14
2015-07-14 677
677







