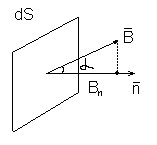
 Магнитным потоком dФ (потоком вектора магнитной индукции) через площадку dS называется произведение площади этой площадки dS и проекции
Магнитным потоком dФ (потоком вектора магнитной индукции) через площадку dS называется произведение площади этой площадки dS и проекции 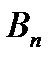 индукции B магнитного поля на направление внешней нормали n площадки dS.
индукции B магнитного поля на направление внешней нормали n площадки dS.
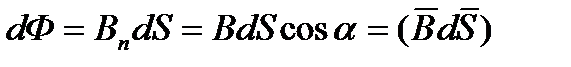
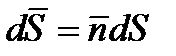
Магнитный поток через поверхность S есть интеграл:
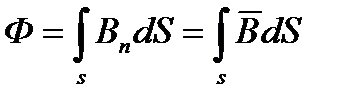
Если поле однородное 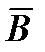 =const., а поверхность плоская и магнитное поле перпендикулярное к поверхности, то:
=const., а поверхность плоская и магнитное поле перпендикулярное к поверхности, то:
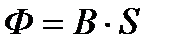
Отсюда вытекает единица измерения магнитного потока в СИ.
[ Ф ]= Вебер (Вб)
Магнитный поток через поверхность равен одному веберу, если площадь поверхности равна одному квадратному метру, магнитное поле с индукцией 1 Тл перпендикулярно поверхности.
1 Вб = 1Тл × 1 м 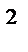
Магнитный поток через поверхность численно равен числу магнитных силовых линий проходящих через эту поверхность или пропорционален числу магнитных силовых линий.
Теорема Остроградского - Гаусса: магнитный поток через любую замкнутую поверхность равна нулю, т.е.
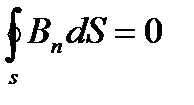
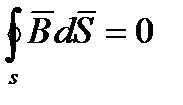
 Теорема Остроградского – Гаусса означает замкнутость магнитных силовых линий, т.е. отсутствие магнитных зарядов, на которых могли бы начинаться и кончаться магнитные силовые линии.
Теорема Остроградского – Гаусса означает замкнутость магнитных силовых линий, т.е. отсутствие магнитных зарядов, на которых могли бы начинаться и кончаться магнитные силовые линии.
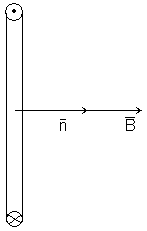
Рассмотрим доказательство теоремы Остроградского – Гаусса для магнитного поля на примере бесконечного прямолинейного проводника с током I.
В качестве поверхности S возьмем круговой цилиндр, с осью совпадающей с током.
Магнитные силовые линии такого тока есть концентрические окружности с центром на оси тока.
Тогда 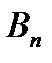 =0 (проекция на направление внешней нормали).
=0 (проекция на направление внешней нормали).
Очевидно, что:
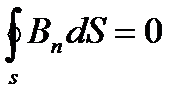
 2015-07-14
2015-07-14 6594
6594
