Сила Лоренца

Сила Ампера действует на проводник с током, но токи направленное упорядоченное движение зарядов. Тогда сила Ампера должна действовать и на отдельные движущиеся заряды. Найдем исходя из силы Ампера выражение для силы действующей на заряд q движущейся со скоростью со стороны магнитного поля с индукцией - сила Лоренца.

Рассмотрим проводник длиной dl и площадью поперечного сечения S в магнитном поле с индукцией . Пусть ток в проводнике – I. Заряд q со скоростью υ, а n₀ – концентрация зарядов. На проводник с током действует сила А. dF⃗=I[dl⃗;B⃗] Покажем теперь, что элемент тока … Idl⃗ по своим свойствам эквивалентен выражениям: qdnυ⃗ Idl⃗=qdnυ⃗ где q – заряд; dn – число зарядов; υ – скорость их движения. Действительно сила постоянного тока I=jS, где S – площадь поперечного сечения; j – плотность тока. Умножим на dl⃗, тогда

Idl⃗=jSdl⃗=j⃗Sdl => Idl⃗=j⃗dV, а j⃗=qn₀υ⃗dV, где n₀dV=dn – число зарядов, тогда Idl⃗=qdnυ⃗ подставим это выражение в формулу для силы Ампера, тогда получим dF⃗=qdn[υ⃗;B⃗] – сила действующая на рассмотриваемый проводник в котором число зарядов dn, тогда сила действующая на один заряд. F⃗_л= ,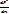

F_л=q[υ⃗;B⃗] – сила Лоренца, знак q учитывается.

F⃗_л Направление силы Лоренца определяется согласно правилу векторного произведения:

сила F_л перпендикулярна площади, в которой лежит υ и В. Направление определяется правилом правого винта. Если вращать рукоятку правого винта от первого вектора υ ко второму вектору В на кратчайший угол α, то поступательное движение винта укажет направление силы Лоренца при положительном заряде F_л=qυBsinα=qυBsin(υ⃗,^B⃗) Выражение для силы Лоренца зависит от выбора системы отсчета: если заряд движется со скоростью в электрическом поле с индукцией , то на заряд будет действовать сила F⃗=qE⃗+q[υ⃗,B⃗].

Т.к. сила Лоренца F_л перпендикулярна к скорости заряда, то она не меняет модуль |υ| и потому сила Лоренца работы не совершает и кинетическую энергию заряда не меняет. Действие силы Лоренца лежит в основе работы ускорителей элементарных частиц. Покажем теперь, что магнетизм есть чисто релятивистский эффект, т.е. для этого покажем, что →0 при →0; F_э=qE. Для этого рассмотрим два точечных заряда q₁ и q₂ движущихся параллельно друг к другу с одинаковой скоростью в вакууме.

F_э= 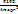ε=μ=1

Сила Лоренца действующая на заряд q₁ в магнитном поле, создаваемом зарядом q₂ равна F⃗_л=q₁[υ⃗,B⃗₂]. Магнитное поле, создаваемое совокупность зарядов dn будет очевидно равно: dB= 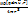. Т.к. по закону Савара- Лапласа: dB⃗= 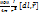, тогда магнитное поле создаваемое одним зарядом: B⃗₂= = 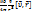подставим теперь В⃗₂ в F⃗_л, тогда F_л= 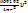, тогда

=μ₀ε₀υ²= , где с= 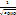=3*10⁸м/с – электродинамическая постоянная => →0, когда →0

Вывод: магнетизм есть чисто релятивистский эффект. В системе Гаусса F⃗=qE⃗+q[ ,B⃗]