Критерий Макнамары

Этот критерий предназначен для работы с данными, полученными в самой простой из номинальных – дихотомической шкале, допускающей два типа ответов – «да» или «нет» (кодируются цифрами 1 и 0 соответственно).

Экспериментальные данные (или данные опроса), полученные педагогом в результате двукратного опроса, записываются в четырехпольную таблицу формата 2х2:

	Второй опрос
Да	Нет
Первый опрос	Да	A	B
Нет	C	D

Поля в этих таблицах заполняются числами:

A – количество учащихся, которые до и после эксперимента ответили «да».

B – количество учащихся, которые до эксперимента ответили «да», а после эксперимента – «нет».

C – количество учащихся, которые до эксперимента ответили «нет», а после эксперимента – «да».

D – количество учащихся, которые до и после эксперимента ответили «нет».

Расчет эмпирического значения M_эмп критерия производится (для B≠C) следующим образом:

а) если B+C=n≤20, то M_эмп находится по таблице M(n,m), где m=min(В,C).

б) если B+C>20, то M_эмп вычисляется по формуле

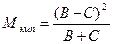
При B=C рекомендуется использовать χ²-критерий.

Опишем алгоритм применения критерия Макнамары следующей схемой:

Найти матрицу

B+C=n≥20

Н0 отклоняется, если Mэмп<Mкр(α)

Вычислить

Mкр(0,05)=3,84 Mкр(0,01)=6,64

Проверить B≠C

B+C<20

Вычислить min(B,C)=m

Найти по таблице Mэмп=M(n,m)

Mкр(0,05)=0,025 Mкр(0,01)=0,005

Нулевая гипотеза H₀={различие значений исследуемого показателя до и после эксперимента несущественно}; альтернативная гипотеза – H₁={различие показателя до и после эксперимента существенно}.

Рассмотрим применение данного критерия на примере.

Проведение пробного тестирования по математике в форме ЕГЭ в первой и второй четверти дало следующие результаты.

		Второе тестирование
Справились	Не справились
Первое тестирование	Справились	A=50	B=19
Не справились	C=31	D=20

Можно ли сказать, что справляемость учащихся изменилась существенно?

В приведенном примере B≠C, поэтому применение критерия Макнамары допустимо. Вычислим сумму B+C=19+31=50>20, поэтому вычисляем:

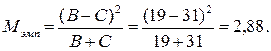
Пусть уровень значимости α=0,05. Тогда M_кр=3,84>2,88=M_эмп. Следовательно, нулевая гипотеза на данном уровне значимости отклоняется, и различия в уровне справляемости существенны.

В предыдущих примерах было показано, каким образом можно оценить существенность изменения того или иного признака на основе сравнения двух выборок. Однако, нередко возникают ситуации, когда необходимо оценить различия сразу в нескольких (более двух) выборках. Для такой цели в математической статистике также имеется ряд критериев достоверности (критерий Крускала-Уоллиса, Фридмана, Пейджа и др.).

Критерий Крускала-Уоллиса H-критерий Крускала-Уоллиса является обобщением U-критерия Манна-Уитни на случай k несвязанных выборок (k>2) и предназначен для оценки различий одновременно между тремя, четырьмя и т.д. выборками по уровню какого-либо признака. Нулевая гипотеза H0={между выборками существует лишь случайные различия по уровню исследуемого признака}. Рассмотрим пример. Одинаковы ли воздействия педагогического эксперимента на младших и старших школьников, а также на учителей по показателям психологической защищённости после эксперимента. Показатель защищённости (номер)                   Младшие подростки 2.8 2.8 2.9 3.1 2.9 2.5 2.7 2.8 2.7 Старшие подростки 3.8 3.1 4.0 3.2 3.8 2.5 3.8 2.9 2.8 Учителя 3.7 3.7 2.8 3.9 3.9 3.6 2.6 3.7 2.7 Проранжируем значения признака для всех групп, как для одной выборки, в порядке возрастания. Далее найдём суммы рангов для каждой группы отдельно (т.е. произведём суммирование рангов по строкам, см. таблицу). Показатель защищённости (номер)                   Сумма рангов Младшие подростки 2.8 2.8 2.9 3.1 2.9 2.5 2.7 2.8 2.7 - Ранг (мл. подростков)       15.5   1.5         Старшие подростки 3.8 3.1 4.0 3.2 3.8 2.5 3.8 2.9 2.8 - Ранг (ст. 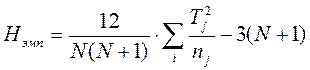подростки)   15.5       1.5         Учителя 3.7 3.7 2.8 3.9 3.9 3.6 2.6 3.7 2.7 - Ранг (учителя)       25.5 25.5           Найдём эмпирическое значение критерия по следующей формуле: , где N – общее количество испытуемых (N=27), Tj – сумма рангов в j-ой строке, nj – число испытуемых в j-ой группе. 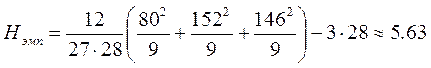В рассматриваемом примере количество испытуемых во всех группах одинаково и равно 9. На практике можно использовать и выборки разных объёмов. 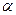По таблице находим критическое значение критерия по уровню значимости и степени свободы k. При этом степень свободы рассчитывается как разность количества групп и единицы. Поэтому в нашем случае k=3-1=2. Примем, что 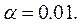Тогда: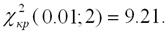 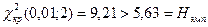Если критическое значение критерия превосходит его эмпирическое значение, то на выбранном уровне значимости следует принять нулевую гипотезу, утверждающую о несущественности различий воздействия на разные группы. В противном случае нулевая гипотеза отвергается. В нашем случае: и нулевая гипотеза на уровне значимости 0.01 принимается. Т.е. воздействие можно считать практически одинаковым во всех группах. Схема применения критерия Крускала-Уоллиса выглядит следующим образом Записать значения признака для каждой из исследуемых групп Посчитать сумму Tj рангов каждой выборки объёма nj Н0 принимается, если Hэмп<Hкр Вычислить Найти для k≥4 и ni≥5 или по специальной таблице для малых k и ni Проранжировать общую выборку по возрастанию