Пусть исходная сеточная функция задана в (n+1)-й точках сетки 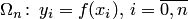 , где
, где 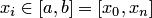 — в общем случае неравноотстоящие узлы, определяемые шагами
— в общем случае неравноотстоящие узлы, определяемые шагами 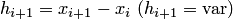 .
.
Воспользуемся сначала кусочным способом. Здесь и далее будем использовать обозначение 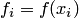 .
.
Выделим "окно" или частичный отрезок 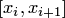 , содержащий только две точки (шаблон
, содержащий только две точки (шаблон 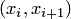 ). Тогда многочлен Лагранжа, интерполирующий исходную функцию на данном шаблоне, имеет вид (где
). Тогда многочлен Лагранжа, интерполирующий исходную функцию на данном шаблоне, имеет вид (где 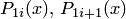 — коэффициенты)
— коэффициенты)
| (4.13) |
Действительно, легко убедиться в том, что 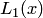 — алгебраический многочлен первой степени, который удовлетворяет условиям функциональной интерполяции (4.3), т.е.
— алгебраический многочлен первой степени, который удовлетворяет условиям функциональной интерполяции (4.3), т.е. 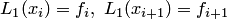 .
.
Выделим "окно" в виде двойного частичного отрезка  c шаблоном
c шаблоном 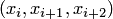 . Тогда многочлен Лагранжа записывается в виде (где
. Тогда многочлен Лагранжа записывается в виде (где 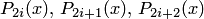 коэффициенты)
коэффициенты)
| (4.14) |
Легко проверить, что (4.14) — многочлен второй степени и также удовлетворяет условиям функциональной интерполяции:
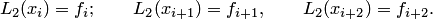
Обобщив запись многочлена на "окно" для к -кратного частичного отрезка 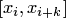 с шаблоном
с шаблоном 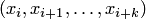 , можно записать многочлен Лагранжа в виде
, можно записать многочлен Лагранжа в виде
| (4.15) |
где 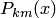 — коэффициенты Лагранжа, которые для внутренних точек шаблона записываются следующим образом:
— коэффициенты Лагранжа, которые для внутренних точек шаблона записываются следующим образом:
| (4.16) |
Легко проверить, что 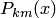 удовлетворяют условию
удовлетворяют условию
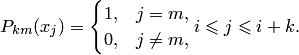
| (4.16) |
Если положить 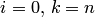 , то приходим к глобальному способу решения задачи. Тогда интерполяционный многочлен Лагранжа n-й степени имеет вид
, то приходим к глобальному способу решения задачи. Тогда интерполяционный многочлен Лагранжа n-й степени имеет вид
| (4.17) |
где коэффициенты Лагранжа 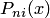 во внутренних точках отрезка записываются в форме
во внутренних точках отрезка записываются в форме
Очевидно, многочлен 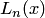 , заданный равенством (4.17), является многочленом степени
, заданный равенством (4.17), является многочленом степени 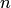 и удовлетворяет функциональным условиям интерполяции (4.3):
и удовлетворяет функциональным условиям интерполяции (4.3): 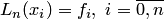 . Для записи интерполяционного многочлена Лагранжа удобно пользоваться табл. 4.1.
. Для записи интерполяционного многочлена Лагранжа удобно пользоваться табл. 4.1.
Здесь 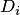 — произведение элементов i-й строки,
— произведение элементов i-й строки, 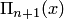 — произведение элементов главной диагонали,
— произведение элементов главной диагонали, 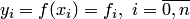 . Тогда многочлен Лагранжа может быть записан в форме
. Тогда многочлен Лагранжа может быть записан в форме
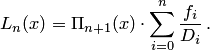
| (4.18) |
 2015-07-14
2015-07-14 515
515








