2015-07-14
882
Как отмечалось выше, выбор сетки и соответствующей степени интерполяционного многочлена при интерполяции сеточных функций является одной из важных задач, решить которую можно, рассмотрев проблему сходимости интерполяционных процессов [6,40] для непрерывных функций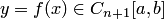 
.
Будем считать, что интерполяция проводится на последовательности сеток
с возрастающим разбиением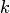 
отрезка 
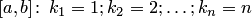и т.д.
Если при данных разбиениях при возрастающем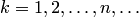 
определяются значения 
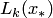в некоторой промежуточной точке 
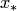, то реализуется интерполяционный процесс, характеризующийся последовательностью значений многочленов: 
.
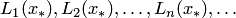Интерполяционный процесс для функции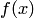 
сходится в точке 
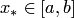, если существует 
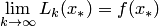(поточечная сходимость).
Для отрезка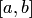 
существует понятие равномерной сходимости в некоторой норме, например max, 
.
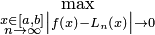Характер сходимости или расходимости интерполяционного процесса зависит как от гладкости и поведения функции 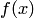, так и от выбора последовательности сеток 
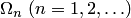. Так, показано, что если f(x) непрерывна на 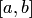, то найдется такая последовательность 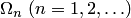, для которой интерполяционный процесс сходится равномерно на 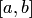(теорема Марцинкевича). Однако для дискретных функций, рассматриваемых в данном разделе, эта теорема не применима. Отметим также, что построены расходящиеся интерполяционные процессы и для формульных функций, например 
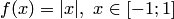и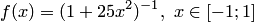 
. Кроме того, применение многочленов высоких степеней приводит к так называемым "провалам" между узлами интерполяции, часто называемым осцилляциями. Указанные свойства интерполяционных процессов обусловливают нецелесообразность применения интерполяционных многочленов высоких степеней. В связи с этим в вычислительной практике для сеточных функций степень 
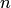не берут выше 
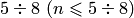и задание частичного отрезка согласуют с выбранной степенью многочлена.
|
|
|
Рассмотрим часто использующиеся на практике линейную и параболическую интерполяцию.
