При определении значения 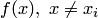 для функции
для функции 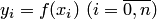 с помощью многочлена Лагранжа возникает погрешность или остаточное слагаемое
с помощью многочлена Лагранжа возникает погрешность или остаточное слагаемое 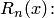
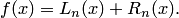
| (4.19) |
Здесь предполагается, что используется глобальный способ интерполяции и что 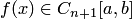 . Последнее предположение требуется для применения соответствующих теорем математического анализа, однако, приведенное ниже соотношение для
. Последнее предположение требуется для применения соответствующих теорем математического анализа, однако, приведенное ниже соотношение для 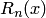 может использоваться и для сеточных функций.
может использоваться и для сеточных функций.
На основе указанных предположений доказано, что при интерполяции функции 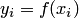 , заданной в общем случае на неравномерной сетке
, заданной в общем случае на неравномерной сетке 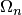 , интерполяционным многочленом Лагранжа
, интерполяционным многочленом Лагранжа 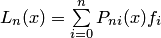 для произвольного значения
для произвольного значения 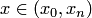 возникает погрешность
возникает погрешность
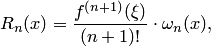
| (4.20) |
где 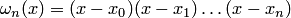 — многочлен (n+1)-й степени, а
— многочлен (n+1)-й степени, а 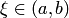 . Поскольку точно найти
. Поскольку точно найти 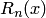 нельзя (из-за неопределенности точки
нельзя (из-за неопределенности точки 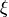 ), то при проведении вычислений обычно находятся только приближенные оценки погрешностей интерполяции, которые являются априорными.
), то при проведении вычислений обычно находятся только приближенные оценки погрешностей интерполяции, которые являются априорными.
Оценка погрешности интерполяции в некоторой произвольной фиксированной точке 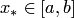 имеет вид, где
имеет вид, где 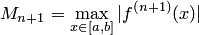
| (4.21) |
Оценка максимальной погрешности интерполяции в любой точке 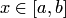 , т.е. на всем отрезке
, т.е. на всем отрезке 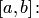
| (4.22) |
Замечание. Для сеточных функций с фиксированными узлами сетки (узлами интерполяции) также можно проводить оценки погрешности по формулам (4.21), (4.22), однако для этого необходимо численно определять 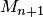 с помощью аппарата численного дифференцирования. При этом следует учитывать, что при вычислении производных высокого порядка возникают большие погрешности.
с помощью аппарата численного дифференцирования. При этом следует учитывать, что при вычислении производных высокого порядка возникают большие погрешности.
▼ Пример 4.2
 2015-07-14
2015-07-14 1373
1373
