1. По расположению заданной точки 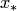 на оси
на оси 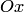 выбрать из всех частичных отрезков
выбрать из всех частичных отрезков 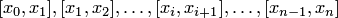 , заданных своими крайними значениями и в совокупности образующих сетку
, заданных своими крайними значениями и в совокупности образующих сетку 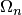 , "окно" интерполяции
, "окно" интерполяции 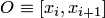 , такое, что
, такое, что 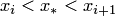 .
.
2. Для отрезка 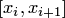 вычислить значения коэффициентов Лагранжа
вычислить значения коэффициентов Лагранжа 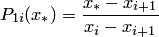 и
и 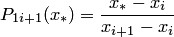 входящих в формулу (4.13) для многочлена
входящих в формулу (4.13) для многочлена 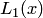 . Правильность полученных значений
. Правильность полученных значений 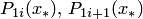 проверить по условию
проверить по условию 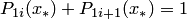 , которое должно выполняться.
, которое должно выполняться.
3. Вычислить искомое значение 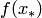 согласно (4.13):
согласно (4.13):
Как показано ниже, порядок этой аппроксимации равен двум, т.е. 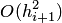 .
.
Геометрическая интерпретация линейной интерполяции при известной формульной функции 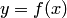 (штриховая линия) изображена на рис. 4.3. Здесь прямая
(штриховая линия) изображена на рис. 4.3. Здесь прямая 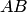 соответствует графику функции
соответствует графику функции 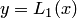 на отрезке
на отрезке 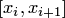 . Приближенное значение функции равно
. Приближенное значение функции равно 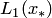 (точка
(точка 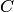 ), и оно отстоит от точного значения
), и оно отстоит от точного значения 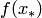 на величину
на величину 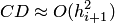 вдоль оси
вдоль оси 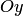 .
.
 2015-07-14
2015-07-14 642
642








