Интерполяционные многочлены Ньютона для равномерной сетки

Сначала рассмотрим решение задачи кусочной интерполяции (применение кусочного способа). Если функция 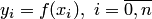задана на равномерной сетке 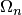, характеризующейся для всех 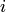, то многочлен (4.29), соответствующий шаблону 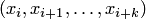, путем подстановки в него вместо разделенных разностей их выражений через конечные разности, согласно (4.28), преобразуется к виду

(4.33)

где 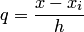— фаза интерполяции, определенная относительно точки 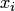; 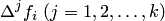— конечные разности.

В соответствии с формулой для фазы интерполяции 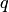точка начала ее отсчета расположена в узле 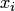и входящие в (4.33) конечные разности относятся к этой же точке 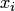. В связи с этим (4.33) удобно применять в начале выделенного шаблона 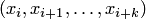, когда 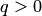. Если 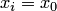, а 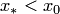, то этот же многочлен используется и для экстраполяции левее точки 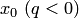. Поэтому многочлен 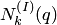называется интерполяционным многочленом для интерполяции вперед (в начале таблицы) или для экстраполяции назад. В (4.33) этот многочлен обозначен цифрой I, указанной в скобках вверху. Для определенности назовем его первым интерполяционным многочленом Ньютона.

Полагая 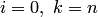, получаем решение задачи глобальной интерполяции на всем отрезке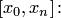

(4.34)

где 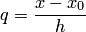. Остаточное слагаемое этого многочлена имеет вид

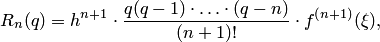
где 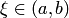— некоторое промежуточное значение между узлами 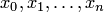и точкой .

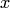Если фазу интерполяции определить относительно 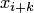некоторой конечной точки шаблона 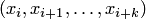, то есть 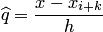, то вместо (4.33) получается второй интерполяционный многочлен Ньютона:

(4.35)

Данный многочлен удобно применять в конце выделенного шаблона или всей таблицы .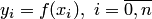

Если 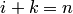, а 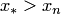, то (4.35) используется для экстраполяции правее точки 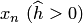. Поэтому многочлен 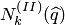называется многочленом для интерполяции назад (в конце таблицы) или экстраполяции вперед.

Полагая 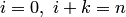, получаем решение задачи глобальной интерполяции — второй интерполяционный многочлен Ньютона n-й степени (где ):

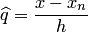(4.36)

Остаточное слагаемое многочлена (4.36) имеет вид

, где .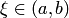

Схема выбора узлов интерполяции при изменении степеней интерполяционных многочленов 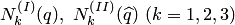в одном алгоритме показана на рис. 4.5. Если точка 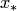находится в начале отрезка 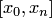, например на частичном отрезке 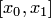, то применяется первый интерполяционный многочлен Ньютона, а если в конце, например на частичном отрезке 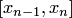, то — второй (рис. 4.5,а). Если точка 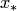находится вдали от концов отрезка , то может применяться как первый интерполяционный многочлен, так и второй (рис. 4.5,б).