2015-07-14
1255
Пусть исходная (интерполируемая) сеточная функция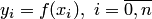 
, задана на неравномерной сетке 
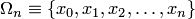, характеризующейся шагами 
.
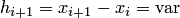Воспользуемся сначала кусочным способом. Из всей совокупности узлов выбираем шаблон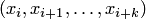 
, соответствующий некоторому "окну" интерполяции 
.
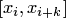Тогда для функциональной интерполяции может быть использован многочлен Ньютона, основанный на разделенных разностях:
| (4.29) |
Действительно,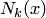 
— многочлен k-й степени, что определяется сомножителями последнего слагаемого (разделенные разности, входящие в качестве одного из сомножителей в эти произведения, есть числа). Кроме того, для многочлена 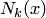удовлетворяются функциональные условия интерполяции: 
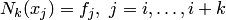. Проверим их справедливость при 
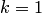(шаблон 
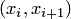) и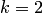 
(шаблон 
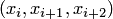). Пусть 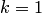. Тогда
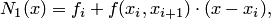
| (4.30) |
и поэтому
Таким образом, условия интерполяции для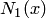 
выполнены, следовательно, многочлен (4.30) может быть использован для линейной интерполяции кусочным способом. Пусть 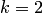. Тогда
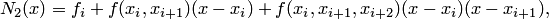
| (4.31) |
и поэтому
Таким образом, условия интерполяции для многочлена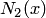 
также выполнены и он может использоваться для параболической интерполяции кусочным способом.
|
|
|
Для произвольного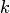 
справедливость равенств 
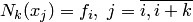, проверяется методом математической индукции.
Полагая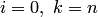 
, приходим к глобальному способу. Тогда интерполяционный многочлен Ньютона n-й степени имеет вид
| (4.32) |
