2015-07-14
653
Разделенные и конечные разности. В практике функционального интерполирования иногда удобнее использовать многочлены Ньютона, степень которых можно последовательно повышать путем добавления очередных слагаемых, имеющих более высокую степень. Такие несимметричные многочлены, альтернативные симметричным многочленам Лагранжа, основаны на разделенных и конечных разностях, вычисляемых по интерполируемой сеточной функции.
Разделенные разности вводятся для функции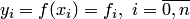 
, заданной на неравномерной сетке 
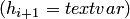, а конечные разности — для функции 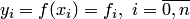, определенной на равномерной сетке 
.
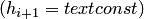Выбрав внутри неравномерной или равномерной сетки соответствующие шаблоны интерполяции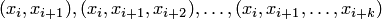 
введем следующие определения разделенных и конечных разностей:
– разделенная разность первого порядка: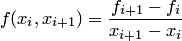 
;
– разделенная разность второго порядка: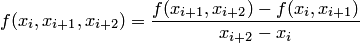 
;
– разделенная разность k-го порядка:;
– конечная разность первого порядка: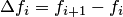 
;
– конечная разность второго порядка: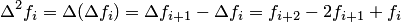 
;
– конечная разность k-го порядка:, где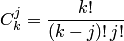 
.
|
|
|
Последовательность получения разделенных и конечных разностей при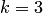 
для произвольной функции наглядно представляют табл. 4.5 и 4.6.
Для гладких функций числовые значения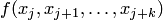 
и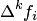 
при возрастании 
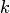уменьшаются и стремятся к нулю, т.е. 
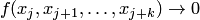и 
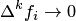при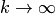 
.
Связь между разделенными и конечными разностями k-го порядка при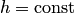 
устанавливается следующим соотношением:
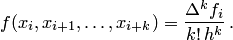
| (4.28) |
Действительно, при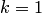 
для разделенной разности 
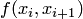получаем 
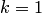, то есть (4.28) при справедливо.
Пусть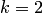 
. Тогда получаем
Таким образом, связь (4.28) выполняется и при 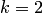. Справедливость (4.28) при произвольном к можно доказать методом математической индукции.
