Ранее было доказано, что вероятность того, что случайная величина X примет значение, принадлежащее интервалу (a; b) равна
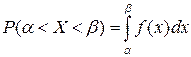
Пусть X – нормально распределенная случайная величина, тогда

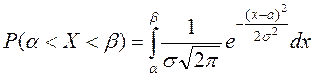
Заменяем 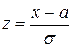
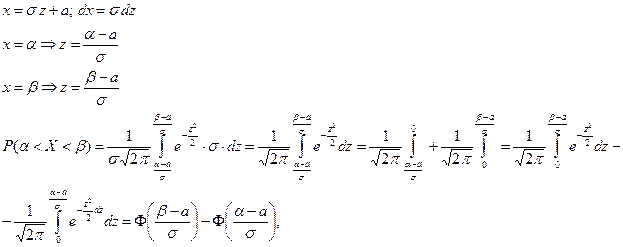
где 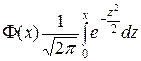 – функция Лапласа (прилож. №2)
– функция Лапласа (прилож. №2)
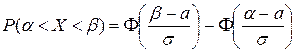 – вероятность попадания нормально распределенной случайной величины в интервал (a; b).
– вероятность попадания нормально распределенной случайной величины в интервал (a; b).
Вероятность заданного отклонения
Вычислим вероятность того, что отклонение нормально распределенной случайной величины X от математического ожидания по абсолютной величине меньше заданного положительного числа d.
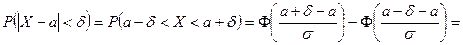
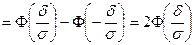
 2015-07-14
2015-07-14 8116
8116








