Нормальная кривая (кривая Гаусса)

График плотности нормального распределения называют нормальной кривой или кривой Гаусса.

Исследуем функцию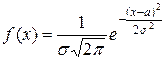

1. Область определения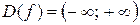

2. Множество значений 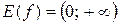(выше оси Ox)

3. 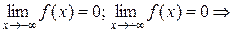ось Ox, т.е. y =0 – горизонтальная асимптота.

4. Интервалы монотонности, экстремумы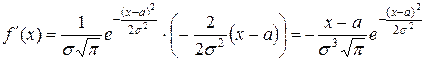

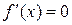при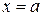

x=a – точка максимума; 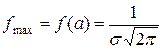. График симметричен относительно прямой x=a.

5. Интервалы выпуклости, вогнутости, точки перегиба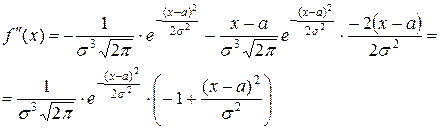

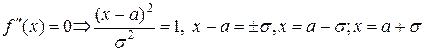
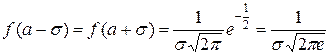
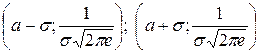– точки перегиба.

6. График

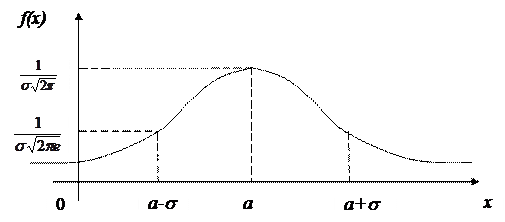Влияние параметров a и s на форму и расположение нормальной кривой

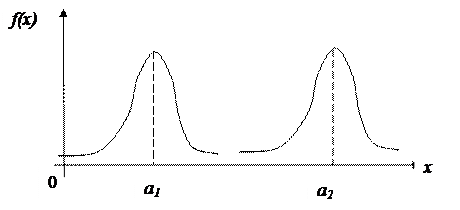
1. Параметр a=M(X) характеризует положение кривой на оси Ox. Если изменять величину a, то нормальная кривая будет смещаться вдоль оси x, не меняя своей формы (если a >0, то сдвиг вправо на a единиц)

2. Параметр s=s(x) характеризует форму нормальной кривой.

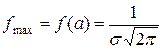
При увеличении s максимальная ордината уменьшается, а при уменьшении s - увеличивается. Площадь, ограниченная кривой распределения f(x) и осью Ox всегда равна 1, значит, при увеличении s нормальная кривая становится более плоской, растягиваясь вдоль оси x, а при уменьшении s нормальная кривая вытягивается вверх, одновременно сжимаясь с боков.

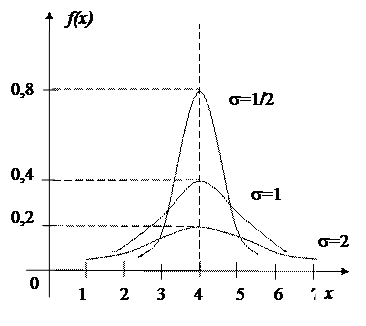Пример.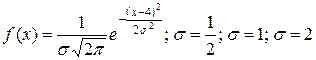

s	max	точки перегиба
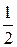	(4; 0,8)	(4,5; 0,48)	(3,5; 0,48)
	(4; 0,4)	(5; 0,24)	(3; 0,24)
	(4; 0,2)	(6; 0,12)	(2; 0,12)