Основные теоремы о пределах. Признаки существования предела

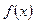Пусть и 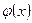– функции, для которых существуют пределы 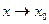(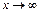): 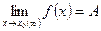и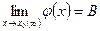

1. Функция не может иметь более одного предела.

2. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е. .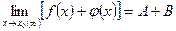

3. Предел произведения конечного числа функций равен произведению пределов этих функций, т.е. .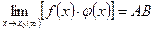

4. Постоянный множитель можно выносить за знак предела.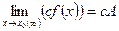

5. Предел частного двух функций равен частному пределов этих функций (при условии, что предел знаменателя не равен нулю), т.е. .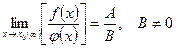

6. Если 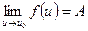, , 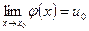то предел сложной функции .

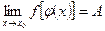7. Если в некоторой окрестности точки 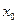(или при достаточно больших значениях х) 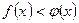, то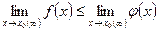

Теорема 1. Если числовая последовательность 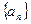монотонна и ограниченна, то она имеет предел.

Теорема 2. Если в некоторой окрестности точки 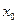(или при достаточно больших значениях х) функция 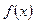заключена между двумя функциям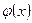и и 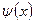, имеющими одинаковый предел А, то функция 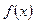имеет тот же предел А