Теорема Ферма. Если дифференцируемая на промежутке Х функция 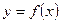 достигает наибольшего или наименьшего значения во внутренней точке
достигает наибольшего или наименьшего значения во внутренней точке 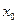 этого промежутка, то производная функции в этой точке равна нулю.
этого промежутка, то производная функции в этой точке равна нулю.
Это означает, что в точке наибольшего или наименьшего значения, достигаемого внутри данного промежутка, касательная к графику функции параллельна оси оХ.
Теорема Ролля. Пусть функция 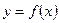 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1) непрерывна на отрезке 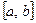 ;
;
2) дифференцируема на интервале 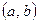 ;
;
3) на концах отрезка принимает равные значения, т.е. 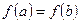 .
.
Тогда внутри отрезка существует по крайней мере одна такая точка 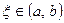 , в которой производная функции равна нулю:
, в которой производная функции равна нулю: 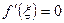 .
.
Теорема Лагранжа. Пусть функция 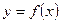 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1) непрерывна на отрезке 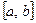 ;
;
2) дифференцируема на интервале 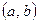 ;
;
Тогда внутри отрезка существует по крайней мере одна такая точка 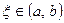 , в которой выполняется равенство:
, в которой выполняется равенство: 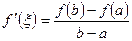 .
.
Теорема (правило) Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле: 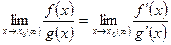 .
.
Правило Лопиталя используется для раскрытия неопределенностей вида 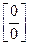 или
или 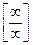 .
.
Правило Лопиталя можно применять также и для раскрытия неопределенностей вида 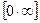 . Для этого произведение
. Для этого произведение 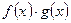 следует представить в виде
следует представить в виде
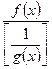 или
или 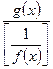 и получить неопределенность
и получить неопределенность 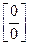 или
или 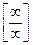 .
.
Пример. 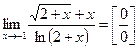
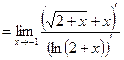
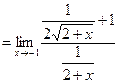
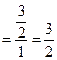
 2015-07-14
2015-07-14 2285
2285








