Достоверное, невозможное и случайное событие. Классическое определение вероятности реализации некоторого события. Статистическое определение вероятности. Геометрическая вероятность.
Случайное событие -- это событие, состоящее из набора элементарных событий. Каждое такое элементарное событие называется благоприятствующим данному случайному событию.
Случайное событие считается наступившим, если наступило одно (любое) из благоприятствующих ему элементарных событий. Так как любой эксперимент оканчивается одним и только одним элементарным событием, случайное событие может произойти, а может не произойти в зависимости от того, является ли произошедшее элементарное событие благоприятствующим ему.
Примерами случайных событий являются достоверные и невозможные события. Достоверное событие -- это случайное событие, которое всегда происходит в результате данного эксперимента. Вероятность достоверного события равна 1. Невозможное событие -- событие, которое никогда не наступает в результате данного эксперимента. Вероятность невозможного события равна 0.
Случайные события -- события, которые при одних и тех же условиях могут произойти,а могут и не произойти. Есть и такие события, которые в данных условиях произойти не могут. Их называют невозможными событиями. Если же событие при данных условиях обязательно произойдет, то его называют достоверным
Чтобы доказать, что данное событие -- случайное, нужно привести пример такой ситуации, или, как говорят математики, такого исхода, когда событие происходит, и пример такого исхода, когда оно не происходит.
Б) Вероятность события. Классическое определение вероятности
Пусть = { 1, 2, …, s} - произвольное конечное пространство элементарных событий, A - событие, состоящее из k элементарных событий: A={ i 1, i 2, …, i k}, 1 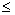 i 1
i 1 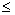 i 2
i 2 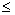 …
… 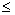 i k
i k 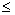 s, k = 1, 2,…, s, и пусть
s, k = 1, 2,…, s, и пусть 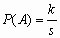 . Определенная таким образом функция P (A) удовлетворяет всем аксиомам 1-4(здесь множество
. Определенная таким образом функция P (A) удовлетворяет всем аксиомам 1-4(здесь множество 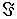 состоит из всех подмножеств множества :
состоит из всех подмножеств множества : 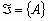 ). Таково классическое определение вероятности события A.
). Таково классическое определение вероятности события A.
Принята следующая формулировка классического определения вероятности: вероятностью события A называется отношение числа исходов, благоприятствующих A, к общему числу исходов.
Из приведенных определений следует: P (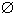 )=0,
)=0, 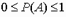 ,
, 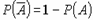 .
.
В) Статистическое определение вероятности.
Будем фиксировать число испытаний, в результате которых появилось некоторое событие А. Пусть было проведено N испытаний, в результате которых событие А появилось ровно nN раз. Тогда число nN называется частотой события, а отношение 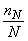 — частостью (относительной частотой) события.
— частостью (относительной частотой) события.
Замечательным экспериментальным фактом является то, что частость события при большом числе повторений испытания начинает мало изменяться и стабилизируется около некоторого определенного значения, в то время как при малом числе повторений она принимает различные, совершенно случайные значения. Поэтому интуитивно ясно, что если при неограниченном повторении испытания частость события будет стремиться к вполне определенному числовому значению, то это значение можно принять и качестве объективной характеристики события А. Такое число Р(А), связанное с событием А, называется вероятностью события А.
Математически неограниченное число повторений испытания записывается в виде предела (lim) при N, стремящемся к бесконечности (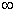 ):
):
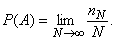
Поскольку nN никогда не может превзойти N, то вероятность оказывается заключенной в интервале 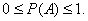
Следует отметить, что приведенное определение вероятности является абстрактным, оно не может быть экспериментально проверено, так как на практике нельзя реализовать бесконечно большое число повторений испытания.
Пусть проводятся независимые испытания, при каждом из которых вероятность события А неизменна. Справедливо утверждение, называемое законом больших чисел или теоремой Бернулли: если N достаточно велико, то с вероятностью сколь угодно близкой к единице, отличие 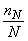 от Р(А) меньше любого наперед заданного положительного числа или, в символьной записи,
от Р(А) меньше любого наперед заданного положительного числа или, в символьной записи, 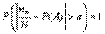 . Т.е. много раз бросая монету, мы “почти наверняка” будем получать примерно равные частоты выпадения герба и цифры.
. Т.е. много раз бросая монету, мы “почти наверняка” будем получать примерно равные частоты выпадения герба и цифры.
Г) Геометрическая вероятность — один из способов задания вероятности; пусть Ω — ограниченное множество евклидова пространства, имеющее объем λ(Ω) (соответственно длину или площадь в одномерной или двумерной ситуации), пусть ω — точка, взятая случайным образом из Ω, пусть вероятность, что точка будет взята из подмножества 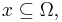 пропорциональна его объёму λ(x), тогда геометрическая вероятность подмножества
пропорциональна его объёму λ(x), тогда геометрическая вероятность подмножества 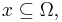 определяется как отношение объёмов:
определяется как отношение объёмов:
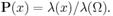
Геометрическое определение вероятности часто используется в методах Монте-Карло, например, для приближённого вычисления значений многократных определённых интегралов.
Если число исходов некоторого опыта бесконечно, то классическое определение вероятности не может служить характеристикой степени возможности наступления того или иного события. В этом случае пользуются геометрическим подходом к определению вероятности. При этом вероятность события 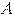 есть отношение меры
есть отношение меры 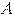 (длины, площади, объема) к мере
(длины, площади, объема) к мере 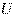 пространства элементарных событий.
пространства элементарных событий.
 2015-08-12
2015-08-12 3789
3789








