Использование дифференциальных уравнений первого порядка при решении некоторых биологических задач(задача о росте численности популяций, задача о переводе вещества в раствор)

6.5.Линейные однородные дифференциальные уравнения второго порядка. Общие свойства их решений. Линейно зависимые и линейно независимые решения. Общее решение.

А-б-г)

Рассмотрим линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка:

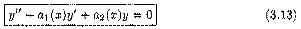
и установим некоторые свойства его решений.

Теорема 3.2. Если функции y₁=y₁(x) и у₂=у₂(х) являются частными решениями уравнения (3.13), то решением этого уравнения является также функция

где c₁ и с₂ - произвольные постоянные.

Подставим функцию у=c₁y₁+с₂у₂ и ее производные в левую часть ЛОДУ (3.13). Получаем:

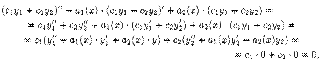
так как функции y₁ и у₂ - решения уравнения (3.13) и, значит, выражения в скобках тождественно равны нулю.

Таким образом, функция у=c₁y₁+c₂y₂ также является решением уравнения (3.13). Из теоремы 3.2, как следствие, вытекает, что если y₁ и у₂ - решения уравнения (3.13), то решениями его будут также функции у=y₁+y₂ и у=cу₁.

Функция (3.14) содержит две произвольные постоянные и является решением уравнения (3.13). Может ли она являться общим решением уравнения (3.13)?

Для ответа на вопрос введем понятие линейной зависимости и линейной независимости функций.

Функции y₁=y₁(x) и у₂=у₂(х) называются линейно независимыми на интервале (а;b), если равенство

где a₁,a₂ є R, выполняется тогда и только тогда, когда a₁=a₂=0.

Если хотя бы одно из чисел a₁ или а₂ отлично от нуля и выполняется равенство (3.15), то функции у₁ и у₂ называются линейно зависимыми на (а;b).

Очевидно, что функции y₁ и у₂ линейно зависимы тогда и только тогда, когда они пропорциональны, т.е. для всех х є (a;b) выполняется равенство 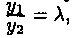или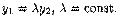

Теорема 3.3. Если дифференцируемые функции y1(x) и у₂(х) линейно зависимы на (а;b), то определитель Вронского на этом интервале тождественно равен нулю.

Так как функции y₁ и у₂ линейно зависимы, то в равенстве (3.15) значение a₁ или а₂ отлично от нуля. Пусть a₁≠0, тогда поэтому для любого х е (а;b)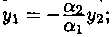

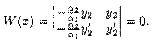
Теорема 3.5 (структура общего решения ЛОДУ второго порядка). Если два частных решения y₁=y₁(x) и у₂=у₂(х) ЛОДУ (3.13) образуют на интервале (а;b) фундаментальную систему, то общим решением этого уравнения является функция

где c₁ и с₂ - произвольные постоянные.

Согласно теореме 3.2, функция (3.16) является решением уравнения (3.13). Остается доказать, что это решение общее, т. е. что из него можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям

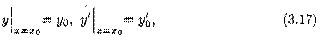
где х_о є (a;b).

Подставив начальные условия (3.17) в решение (3.14), получим систему уравнений

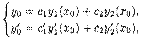
где у_о=у(х_о), у_о=у'(х_о), с неизвестными с₁ и с_2. Определитель этой системы

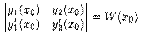
равен значению вронскиана W(x) при х=х_о.

Так как решения y1(x) и у₂(х) образуют фундаментальную систему решений на (а; b) и хо є (а;b), то, согласно теореме 3.4, W(x₀)≠0. Поэтому система уравнений имеет единственное решение:

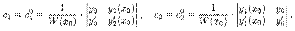
Решение у=c⁰₁y₁(x)+c₀₂y₂(x) является частным решением (единственным, в силу теоремы единственности) уравнения (3.13), удовлетворяющим начальным условиям (3.17). Теорема доказана.

Пример 3.5. На основании теоремы 3.5 общим решением уравнения у"+у=0 (см. пример 3.4) является функция у=c₁sinx+с₂cosx.

В) Функции y ₁(x), y ₂(x), …, y _n (x) называются линейно зависимыми на отрезке [ а, b ], если существуют действительные числа m ₁, m ₂, …, m _n не все равные нулю, такие, что для всех х 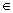[ а, b ] выполняется тождество

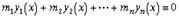
и называются линейно независимыми, если тождество выполняется лишь в случае, когда m ₁ = m ₂= … = m _n = 0.

Практически определить линейную зависимость или независимость частных решений y ₁, y ₂, …, y _n ДУ можно, используя определитель Вронского (Вронскиан):

.

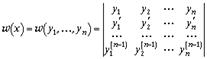В случае линейной зависимости функций y ₁, y ₂, …, y _n определитель Вронского тождественно равен нулю, в случае их линейной независимости – определитель Вронского не равен нулю ни в одной точке отрезка [ а, b ]