Для опису збіжності обчислювального процесу й оцінки  погрішності наближеного рішення необхідні додаткові поняття.
погрішності наближеного рішення необхідні додаткові поняття.
Поняття норми. Нормою вектора х, позначається 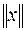 , називається величина,що задовольняэ умовам:
, називається величина,що задовольняэ умовам:
1. 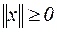 ;
;
2. 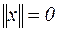

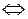 х=0; (3.6)
х=0; (3.6)
3. 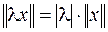 ;
;
4. 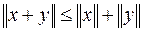 .
.
У теорії метричних просторів одержали поширення наступні типи норм:
1. 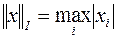 ;
;
2. 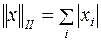 ;
;
3. 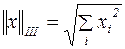 .
.
Залежно від типу геометричної фігури, одержуваної в тривимірному просторі, описуваної умовою 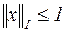 , перша з них називається кубічною, друга,- октаедрическою і третя,- сферичною.
, перша з них називається кубічною, друга,- октаедрическою і третя,- сферичною.
Нормою матриці А, позначається 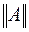 , називається величина, що задовольняє крім вимог (3.6) додатковій умові
, називається величина, що задовольняє крім вимог (3.6) додатковій умові
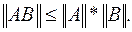
Звичайно, використовуються одна з наступних норм:
1. 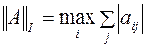 ;
;
2. 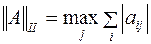 ;
;
3. 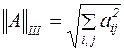 .
.
При одночасному використанні норм необхідно їхнє узгодження. А саме, норма вектора першого типу використовується з нормою матриці першого типу й т.д.
Поняття відстані. Відстанню між векторами x, y, позначається символом 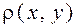 , називається величина
, називається величина
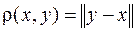 .
.
Із властивості 4 (3.6) треба важливе для подальшого, так зване, нерівність трикутника
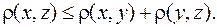
Дійсно,
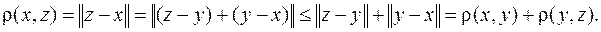
Стискаючі відображення. Нехай F,- деяке відображення в лінійному просторі векторів. Воно називається стискаючої,- якщо існує таке число 
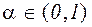 , що для будь-яких векторів x, y виконується співвідношення
, що для будь-яких векторів x, y виконується співвідношення
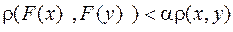 .
.
Стосовно до нормальної форми системи рівнянь (3.3) у якості F розглянемо праву частину системи рівнянь. А саме,
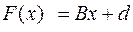 .
.
Тоді
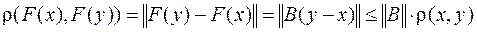 .
.
Таким чином, для того, щоб відображення, обумовлене системою (3.3) було стискаючої досить, щоб одна з норм матриці В була менше 1.
Поняття збіжності. Нехай 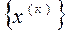 , де до = 1, 2, …,- деяка нескінченна послідовність векторів. Говорять, що вона сходиться до вектора х по нормі, якщо
, де до = 1, 2, …,- деяка нескінченна послідовність векторів. Говорять, що вона сходиться до вектора х по нормі, якщо
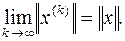
Послідовність 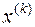 сходиться до вектора
сходиться до вектора 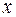 покомпонентно, якщо
покомпонентно, якщо
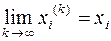 для
для 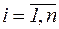 .
.
Неважко показати, що два ці поняття до певної міри еквівалентні. А саме, якщо послідовність 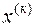 сходиться по нормі, то вона сходиться покомпонентно й навпаки.
сходиться по нормі, то вона сходиться покомпонентно й навпаки.
При аналізі збіжності послідовностей центральне місце належить ознаці Коші:
Послідовність 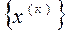 сходиться тоді й тільки тоді, коли для сходиться тоді й тільки тоді, коли для 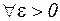 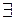 такий номер такий номер 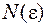 , що для , що для 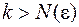 й й 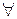 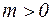 виконується виконується
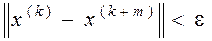 (або
(або 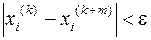 для для 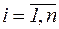 ). ).
|
Збіжність ітераційного процесу. Оцінка погрішності. Нехай 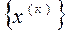 ,- ітераційна послідовність, тобто
,- ітераційна послідовність, тобто
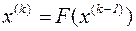 , (3.7)
, (3.7)
де 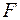 ,- стискаюче відображення з коефіцієнтом стиску
,- стискаюче відображення з коефіцієнтом стиску 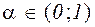 .
.
Розглянемо 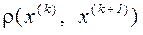 . По індукції маємо
. По індукції маємо
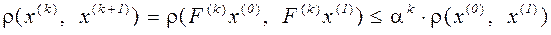 . (3.8)
. (3.8)
Далі, по властивості трикутників і з обліком (3.8), справедливим виявляється співвідношення
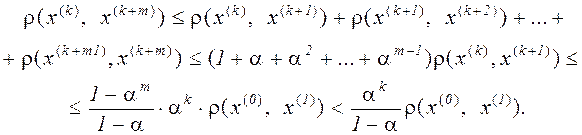 (3.9)
(3.9)
Зажадавши тепер, щоб
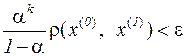 ,
,
очевидно, можна знайти номер 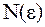 , починаючи з якого
, починаючи з якого 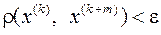 для
для 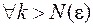 , m > 0.
, m > 0.
Таким чином, для стискаючого відображення ознака Коші виконаний і, отже, ітераційний процес (3.7) сходиться.
Оцінимо тепер погрішність до- го наближення, а саме, величину 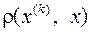 , де х- х - точне рішення. Із цією метою розглянемо співвідношення (див. (3.9))
, де х- х - точне рішення. Із цією метою розглянемо співвідношення (див. (3.9))
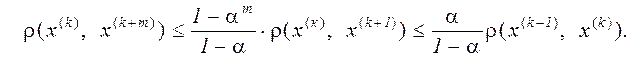
Переходячи в ньому до межі при 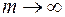 , одержимо, таким чином,
, одержимо, таким чином,
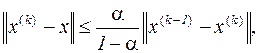 (3.10)
(3.10)
і доведеним стає твердження:
| Якщо одна з норм матриці B системи рівнянь (3.3) менше одиниці, то ітераційний процес (3.4) є збіжним при будь-якому початковому наближенні. Погрішність до- го наближення описується співвідношенням (3.10). |
3.5 Приведення системи Ax=b до нормального виду
З попереднього треба, що успіх наближеного рішення системи лінійних алгебраїчних рівнянь (3.1) багато в чому визначається можливістю її приведення до нормального виду (3.3), для якого виконується достатні умови збіжності. Приведемо деякі розумiння й рекомендації на цей рахунок.
Перший варіант. Розглянемо систему
Ах=b.
Представимо матрицю А в виді суми А=А1+А2, де det А1 ≠ 0. Тоді
(А1+А2) x=b,
звідси
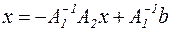 .
.
Позначивши через 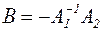 ,
, 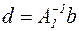 , одержимо
, одержимо
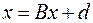 ,
,
що й було потрібно. Тоді для того, щоб забезпечити виконання достатньої умови збіжності 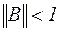 , у якості А1 досить взяти матрицю близьку до А, тобто А1≈А, у якості А2, - «малу» матрицю
, у якості А1 досить взяти матрицю близьку до А, тобто А1≈А, у якості А2, - «малу» матрицю 
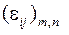 .
.
Пояснимо цю пропозицію на прикладі. Розглянемо
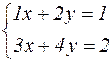 ,
,
Тут 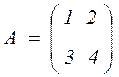 . Нехай
. Нехай
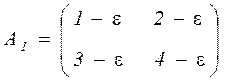 ,
,
Тоді 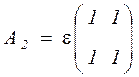 . Знайдемо
. Знайдемо 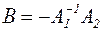 .
.
Маємо det А1 = -2 ≠ 0 і
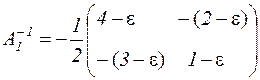 .
.
Тоді
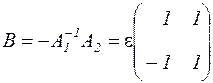
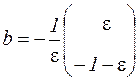
і система приймає вид
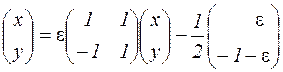 .
.
Очевидно, для збіжності методу ітерацій досить взяти 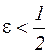 .
.
Другий варіант. Полягає в наступному. Шляхом еквівалентних перетворень намагаються домогтися того, щоб діагональні елементи в матриці А домінували в лівій частині відповідних рівнянь, тобто були по модулі істотно більше інших. Після цього кожне з рівнянь ділять на 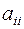 й, перше рівняння дозволяють відносно
й, перше рівняння дозволяють відносно 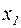 друге,- відносно
друге,- відносно 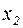 й т.д.
й т.д.
Як приклад розглянемо наступну систему
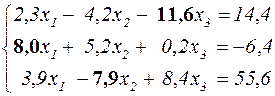
У результаті аналізу коефіцієнтів лівої частини рівнянь виробляється їхня перестановка
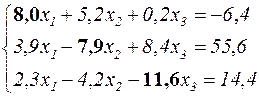
і для забезпечення домінування в другому рівнянні коефіцієнта 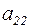 , що поки дорівнює -7,9, до другого рівняння додається третє. У результаті цього маємо
, що поки дорівнює -7,9, до другого рівняння додається третє. У результаті цього маємо
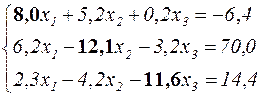
або, у нормальній формі,
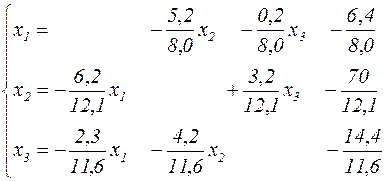 .
.
Тут матриця
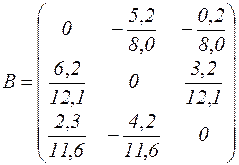 ,
,
очевидно, її норма 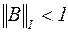 , і, отже, формований нею ітераційний процес сходиться.
, і, отже, формований нею ітераційний процес сходиться.
Третій варіант. Є обґрунтованим теоретично, формалiзуємим і, із цієї причини, мабуть, найбільш зручним. Він полягає в наступному.
Розглянемо систему (3.11)
Ax=b
і припустимо, що det А1 ≠ 0. Помножимо обидві частини на 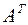 , одержимо
, одержимо
A1 x=b1,
де A1=АТА, b1= AT b. Тут матриця A1 є симетричною, тобто 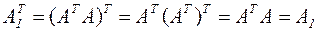 , причому її діагональні елементи
, причому її діагональні елементи 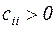 , у противному випадку, принаймні, один зі стовпців матриці А дорівнює нулю й, отже, det А = 0. Далі, ділячи рівняння на діагональні елементи
, у противному випадку, принаймні, один зі стовпців матриці А дорівнює нулю й, отже, det А = 0. Далі, ділячи рівняння на діагональні елементи 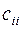 й, дозволяючи їх відносно
й, дозволяючи їх відносно 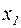 ,
, 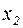 і т.д. одержимо нормальну систему
і т.д. одержимо нормальну систему
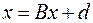 ,
,
де 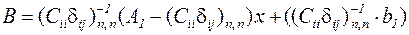 .
.
Показано, що для нормальної системи, отриманої таким чином, метод Зейделя сходиться.
 2015-08-21
2015-08-21 662
662








