Розглянемо рівняння (4.1). Нехай 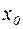 - деяке наближення до його рішення. Розкладемо ліву частину рівняння по формулі Тейлора в точці
- деяке наближення до його рішення. Розкладемо ліву частину рівняння по формулі Тейлора в точці 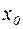
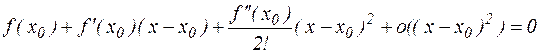 . (4.2)
. (4.2)
Метод Ньютона. Обмежимося в розкладанні (4.2) першими двома доданками
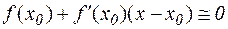
і розв'яжимо отримане вираження відносно х
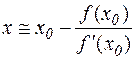 .
.
Останнє співвідношення приймається в якості базового для формування обчислювального процесу. Він описується формулою
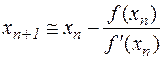
| (4.3) |
і називається методом Ньютона. Помітимо, що правило (4.3) має цілком певний геометричний зміст.
Дійсно, розглянемо рівняння дотичної до графіка функції 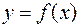 в точцi
в точцi 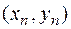
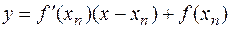
і визначимо її точку перетинання з віссю ох. Маємо 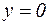 , звідки
, звідки
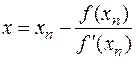 .
.
З порівняння отриманого вираження з (4.2) слiдує висновок, що
абсциса точцi перетинання дотичній, проведеної до графіка функції в точці 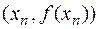 і являє собою наступне наближення до рішення рівняння (4.1) (Малюнок 4.2). і являє собою наступне наближення до рішення рівняння (4.1) (Малюнок 4.2).
|
 |
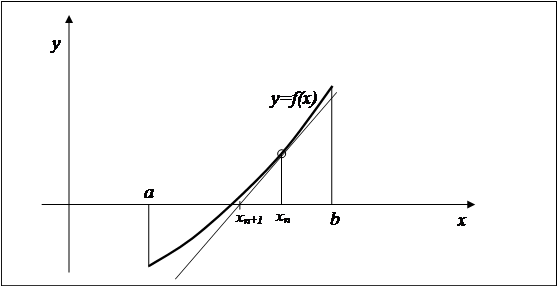
Рисунок 4.2. Метод Ньютона
Із цієї причини метод Ньютона називають ще методом дотичних.
Метод хорд. Розглянемо (4.3). Замінимо в ньому
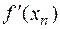 на
на 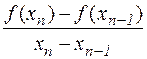 .
.
У результаті цього одержимо нове обчислювальне правило
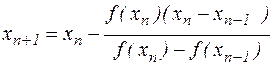
| (4.4) |
називане методом хорд.
З'ясуємо його геометричний зміст.
Розглянемо точки кривої 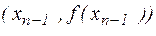 ,
, 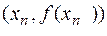 і проведемо через них пряму
і проведемо через них пряму
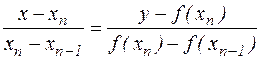 .
.
Знайдемо, далі, її точку перетинання з віссю абсцис. Маємо
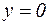 ,
, 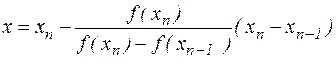 .
.
Порівнюючи отримані вираження зі співвідношенням (4.4), доходимо висновку, що
| абсциса точки перетинання прямій, що проходить через точки кривій, обумовлені двома останніми наближеннями, являє собою наступне наближення до рішення рівняння (4.1) (Малюнок 4.3). |
 |
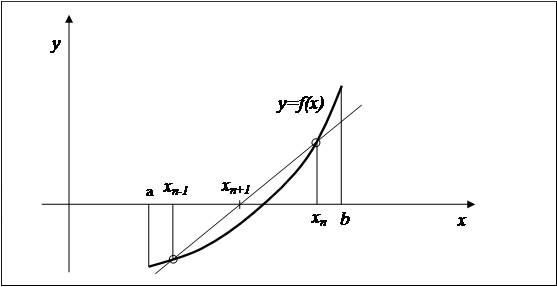
Рисунок 4.3. Метод хорд
 Збіжність, оцінка погрішності. Розглянемо ці питання на прикладі методу Ньютона.
Збіжність, оцінка погрішності. Розглянемо ці питання на прикладі методу Ньютона.
Розглянемо відображення
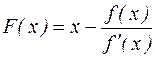 ,
,
де 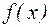 , - ліва частина рівняння (4.1),
, - ліва частина рівняння (4.1), 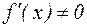 .
.
Помітимо, що нерухома точка відображення 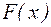 , якщо вона є, є й рішенням рівняння (4.1). Дійсно, нехай існує значення х таке, що
, якщо вона є, є й рішенням рівняння (4.1). Дійсно, нехай існує значення х таке, що 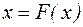 . Звідси
. Звідси
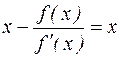 ,
,
звідки 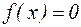 , що й було потрібно.
, що й було потрібно.
Далі, нехай 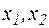 , - довільні значення х, оцінимо величину
, - довільні значення х, оцінимо величину 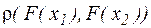 . Маємо
. Маємо
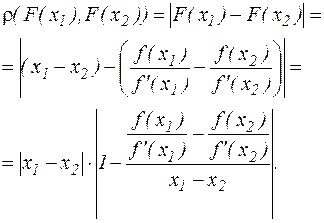
Тоді по теоремі Лагранжа
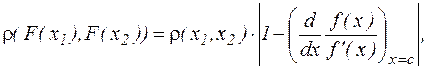
де 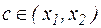 , або
, або
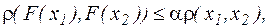
де 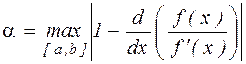 .
.
Звідси слiдує твердження.
Якщо 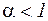 або, що то ж або, що то ж 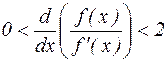 , то відображення , то відображення 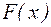 є стискаючим, послідовність (4.3), їм формована,є збіжною й, отже, метод дотичних у цьому випадку сходиться. є стискаючим, послідовність (4.3), їм формована,є збіжною й, отже, метод дотичних у цьому випадку сходиться.
|
Гранична точка х послідовності (4.3) є нерухомою точкою відображення 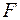 і є шуканим рішенням. Погрішність
і є шуканим рішенням. Погрішність 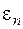 , - n- го наближення до рішення, як і раніше, описується співвідношенням (3.10).
, - n- го наближення до рішення, як і раніше, описується співвідношенням (3.10).
 2015-08-21
2015-08-21 297
297








