Передбачається, що система рівнянь представлена у вигляді
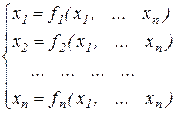 , (5.1)
, (5.1)
де 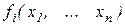 , - функції, що диференціюються,змінних
, - функції, що диференціюються,змінних 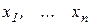 в області D, що містить рішення системи (5.1). Позначивши через
в області D, що містить рішення системи (5.1). Позначивши через 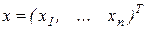 і
і 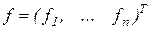 , систему (5.1) можна представити в більше зручному для викладу виді
, систему (5.1) можна представити в більше зручному для викладу виді
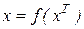 .
.
Нехай 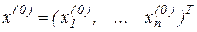 , - деяке наближення до шуканого рішення. Тоді обчислювальний процес, организовуваний по формулі
, - деяке наближення до шуканого рішення. Тоді обчислювальний процес, организовуваний по формулі
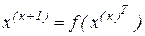 , (5.2)
, (5.2)
де k = 0, 1, 2, … називається методом ітерацій. Якщо при обчисленні чергової координати k+1 – го наближення використовувати обчислені перед цим значення попередніх координат цього ж наближення, одержимо модифікацію, називану методом Зейделя. У ній алгоритм обчислень описується в такий спосіб
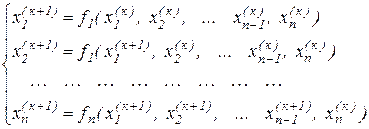 .
.
За певних умов метод ітерацій (5.2) сходиться до точного рішення системи (5.1). Установимо ці умови, використовуючи, як і вище, поняття стискаючого відображення.
В n- мірному просторі 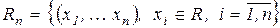 набір функцій
набір функцій 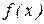 визначає деяке відображення,, що нескiнченно диференціюється. Вище (див. Лекція 3) було показано, що збіжність ітераційної послідовності забезпечується збіжністю утворюючого її відображення.
визначає деяке відображення,, що нескiнченно диференціюється. Вище (див. Лекція 3) було показано, що збіжність ітераційної послідовності забезпечується збіжністю утворюючого її відображення.
Нехай 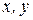 - довільні точки
- довільні точки 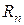 , оцінимо
, оцінимо 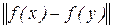 . Припустимо, що величина
. Припустимо, що величина 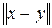 досить мала й у тейлоровських розкладаннях функцій
досить мала й у тейлоровських розкладаннях функцій 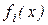 у точцi
у точцi 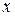 дозволено обмежитися величинами першого порядку малості. Тоді
дозволено обмежитися величинами першого порядку малості. Тоді
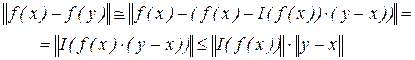 ,
,
де
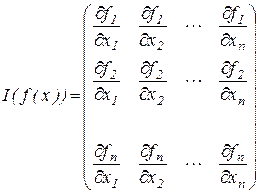 , (5.3)
, (5.3)
- матриця Якобi системи функцій 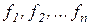 .
.
Якщо 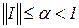 в області D, відображення
в області D, відображення 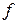 є стискаючим і є підстави вважати, що ітераційний процес (5.2) сходиться до рішення системи (5.1). Більш виразно це формулюється у вигляді наступної теореми:
є стискаючим і є підстави вважати, що ітераційний процес (5.2) сходиться до рішення системи (5.1). Більш виразно це формулюється у вигляді наступної теореми:
Нехай в області D система (5.1) має, принаймні, одне рішення, що належить її внутрішньої частини й норма матриці Якобi в замиканні 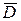 області D менше одиниці. Тобто,
області D менше одиниці. Тобто, 
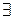 таке
таке 
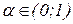 , що
, що 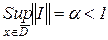 . Тоді в області D система (5.1) має рішення й ітераційний процес (5.2) сходиться до одному з рішень при будь-якому
. Тоді в області D система (5.1) має рішення й ітераційний процес (5.2) сходиться до одному з рішень при будь-якому
виборі початкового наближення 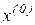 .
.
Погрішність k - го наближення, як і раніше (див. Лекція 3), можна оцінити співвідношенням
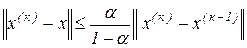 .
.
Зауваження. Нерідко вихідна система рівнянь буває представленої в неявній формі
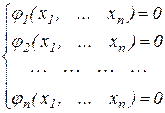 , (5.4)
, (5.4)
де якобiан системи
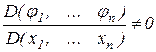 .
.
Тоді для приведення (5.4) до виду (5.1), що забезпечує збіжність, можна використовувати припущування, аналогічні висловленим вище (див. Лекція 4). А саме, помножимо обидві частини (5.4) на деяку неособливу квадратну матрицю А
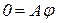 ,
,
додамо, далі до обох частин х
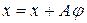 ,
,
позначимо
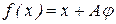
і зажадаємо, щоб
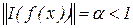 .
.
Із цього співвідношення можна визначити коефіцієнти матриці А. Якщо це зробити важко для всієї області D, то зазначену операцію можна робити покроково на кожному кроці ітераційного процесу.
Пояснимо це на прикладі двох рівнянь
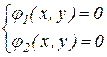 .
.
Позначимо
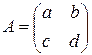 .
.
Тоді система (5.1) приймає вигляд
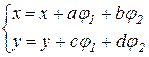 .
.
Звідси
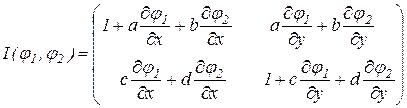 .
.
Задамо далі, 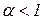 і зажадаємо, щоб
і зажадаємо, щоб
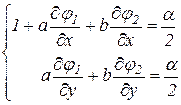 .
.
Звідси, за правилом Крамера, наприклад,
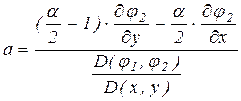 ,
,
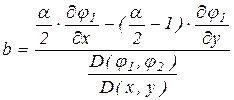 .
.
Аналогічним чином, зажадавши
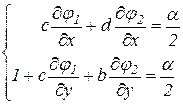
Знайдемо с и d.
Проводячи зазначені перетворення на кожному кроці ітераційного процесу, тим самим створюємо умови для збіжності його зі швидкістю 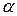 в цілому.
в цілому.
 2015-08-21
2015-08-21 307
307







