У цьому випадку рівняння (4.1) приводиться до виду
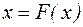 (4.5)
(4.5)
Далі, вибирається початкове наближення 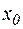 до рішення й на основі (4.5) за правилом
до рішення й на основі (4.5) за правилом
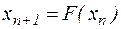 (4.6)
(4.6)
будується послідовність 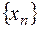 .
.
Розглянемо відображення, формоване функцією 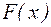 . Нехай
. Нехай 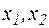 , - деякі довільні значення змінної
, - деякі довільні значення змінної 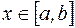 , оцінимо величину
, оцінимо величину 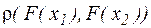 . Маємо
. Маємо
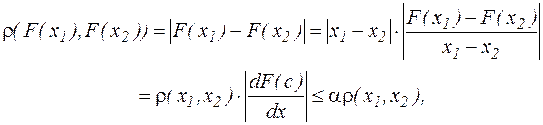
де 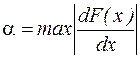 .
.
Звідси випливає наступне твердження.
Якщо 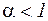 або те ж або те ж 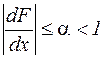 для для 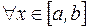 , то відображення , то відображення 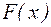 є стискаючим. Отже, ітераційний процес у цьому випадку сходиться. є стискаючим. Отже, ітераційний процес у цьому випадку сходиться.
|
Погрішність n- го наближення визначається співвідношенням (3.10).
Зупинимося на закінчення на процедурі приведення рівняння (4.1) до виду (4.5). Один з її варіантів полягає в наступному:
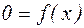 - вихідне рівняння;
- вихідне рівняння;
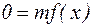 - де m, - підлягаючому визначенню параметр;
- де m, - підлягаючому визначенню параметр;
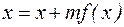 - нова форма рівняння;
- нова форма рівняння;
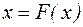 , де
, де 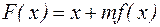 - необхідна форма.
- необхідна форма.
Нарешті, значення параметра m вибирається з умови
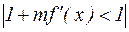
для 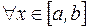 .
.
 2015-08-21
2015-08-21 551
551








