Розглянемо два з них.
Метод послідовних наближень. Представимо в рівнянні (1) 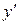 у вигляді відносини диференціалів
у вигляді відносини диференціалів 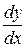 , тоді
, тоді
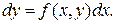
Далі, інтегруючи обидві частини отриманого співвідношення на проміжку [ x0, x ] одержуємо
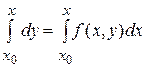 ,
,
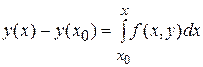
або
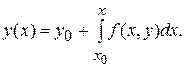 (3)
(3)
Співвідношення (3) являє собою інтегральне рівняння, еквівалентне задачі (1), (2). На його основі будується наступний обчислювальний процес
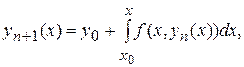 (4)
(4)
де 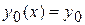 , що і називається методом послідовних наближень. За певних умов послідовність функції
, що і називається методом послідовних наближень. За певних умов послідовність функції 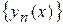 сходиться до точного рішення задачі (1), (2). А саме,
сходиться до точного рішення задачі (1), (2). А саме,
Нехай у прямокутнику 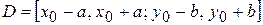 виконані умови теореми існування й одиничності й
виконані умови теореми існування й одиничності й 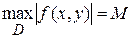 . Тоді в проміжку
. Тоді в проміжку 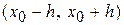 , де
, де 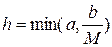 послідовність (4) сходиться до точного рішення. Причому справедливо наступну оцінку
послідовність (4) сходиться до точного рішення. Причому справедливо наступну оцінку

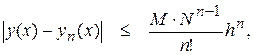
де 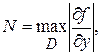
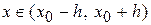 .
.
Для ілюстрації цього методу розглянемо наступний
Приклад. Знайти рішення задачі Коші
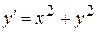 ,
, 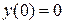 .
.
Знайти два перших наближення до рішення, оцінити погрішність.
Рішення. Візьмемо як область 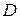 квадрат [-1, 1; -1, 1]. Тут
квадрат [-1, 1; -1, 1]. Тут 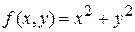 ,
, 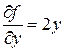 ,
, 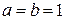 . Тоді
. Тоді
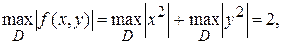
т.е. М=2,
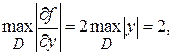
т.е. N=2,
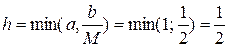 .
.
Погрішність n- го наближення
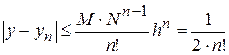 ,
,
звідси погрішність другого,- 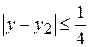 .
.
Знайдемо наближення 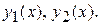 Думаючи, що
Думаючи, що 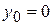 , з (4) маємо
, з (4) маємо
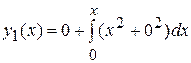 ,
,
т.е. 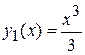 .
.
Тоді
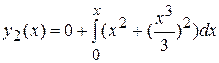
т.е.
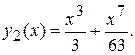
Зауваження. У тому випадку, коли дана погрішність 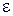 наближеного рішення число ітерацій, тобто послідовних наближень, можна знайти, зажадавши
наближеного рішення число ітерацій, тобто послідовних наближень, можна знайти, зажадавши
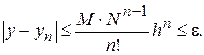
Так, наприклад, у розглянутому прикладі
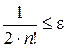 ,
,
звідки 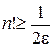 й значення
й значення 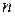 встановлюється послідовним перебором.
встановлюється послідовним перебором.
Метод рядів Тейлора. У цьому випадку рішення задачі (1), (2) шукається у вигляді ряду
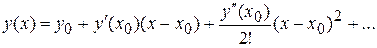 .
.
Значення похідних, необхідних для побудови рішення перебувають шляхом послідовного диференціювання рівняння (1). Так, безпосередньо з нього треба
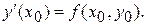
Далі,
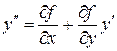 ,
,
тоді
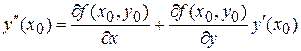
і т.д.
Очевидно, що дана процедура дозволяє одержати рішення з як завгодно високою точністю лише в тому випадку, коли функція 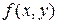 є нескінченно дифференцируемой у крапці
є нескінченно дифференцируемой у крапці 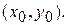 В противному випадку даний метод може бути взагалі не застосуємо. Див., наприклад, задачу
В противному випадку даний метод може бути взагалі не застосуємо. Див., наприклад, задачу
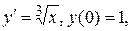
де 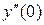 вже не існує.
вже не існує.
 2015-08-21
2015-08-21 308
308








