Класифікація методів. Виробляється залежно від особливостей тої інформації, що використовується при обчисленні наближеного значення y(x) у вузловій крапці.
У першому наближенні правило, по якому відбуваються обчислення символічно можна представити у вигляді
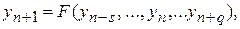 (5)
(5)
де
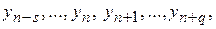 - наближені значення рішення задачі (1), (2) у крапках
- наближені значення рішення задачі (1), (2) у крапках 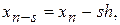
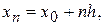
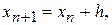
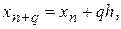
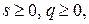
h – крок інтегрування. Якщо
1) 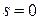 , а
, а 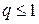 , те правило (5) називається однокроковим, у противному випадку,- багатокроковим;
, те правило (5) називається однокроковим, у противному випадку,- багатокроковим;
2) 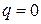 , обчислювальне правило називається явним, при
, обчислювальне правило називається явним, при 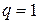 неявним, при
неявним, при 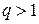 , - із забіганням уперед.
, - із забіганням уперед.
Далі, основну увагу приділимо однокроковим методам. Відповідне обчислювальне правило має вигляд
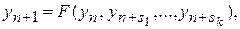
де 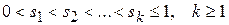 .
.
Методи, засновані на розкладанні в ряд Тейлора. Припустимо, що вузли інтегрування є рівновіддаленими, тобто 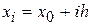 й розглянемо ділянку
й розглянемо ділянку 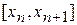 . Припускаючи функцію
. Припускаючи функцію 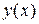 дифференцируемую достатнє число раз, маємо
дифференцируемую достатнє число раз, маємо
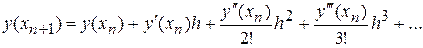 (6)
(6)
Обмежуючись малими першого порядку відносно h, одержимо правило
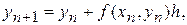 (7)
(7)
яке називається явним методом Эйлера. Його погрішність на відрізку 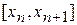 становить
становить
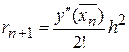 ,
,
де 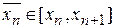 , а на кінцевому відрізку [ a, b ] з огляду на
, а на кінцевому відрізку [ a, b ] з огляду на 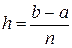 , дорівнює
, дорівнює
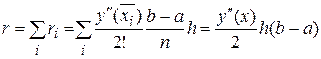 ,
,
де 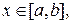
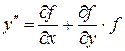 . На підставі цього даний метод називається методом першого порядку точності. Він має наочну геометричну інтерпретацію (Малюнок 1) і називається також методом ламаних. На кожній ділянці довжиною h ділянка інтегральної кривої заміняється відрізком прямої.
. На підставі цього даний метод називається методом першого порядку точності. Він має наочну геометричну інтерпретацію (Малюнок 1) і називається також методом ламаних. На кожній ділянці довжиною h ділянка інтегральної кривої заміняється відрізком прямої.
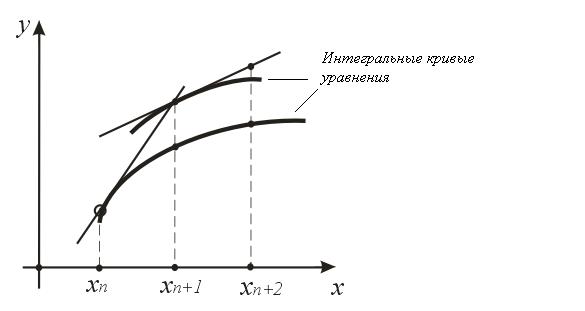
Малюнок 1. Явна схема Эйлера.
Зауваження 1. Якщо скористатися розкладанням
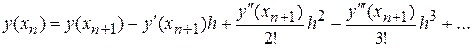 (8)
(8)
і також обмежитися малими першого порядку, одержимо правило
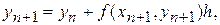 (9)
(9)
яке називається неявною схемою Эйлера.
Погрішність формули (9) дорівнює
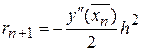 ,
,
погрішність методу на кінцевому проміжку 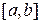
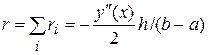 .
.
Зауваження 2. Складемо (7), (9) і розділимо на два, у результаті чого одержимо нове правило
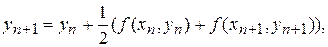 називане методом трапецій. Також як і (9) воно є неявним. Якщо з розкладання (6) почленно відняти розкладання (8), одержимо локальну погрішність формули трапецій
називане методом трапецій. Також як і (9) воно є неявним. Якщо з розкладання (6) почленно відняти розкладання (8), одержимо локальну погрішність формули трапецій
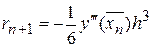 .
.
Тоді погрішність, що накопичується на відрізку 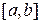 буде дорівнює
буде дорівнює
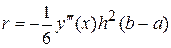 ,
,
де 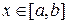 . Таким чином, метод трапецій має другий порядок точності.
. Таким чином, метод трапецій має другий порядок точності.
Зауваження 3. Розглянуті вище погрішності наближених методів описують ті помилки, які виникають внаслідок заміни диференціального рівняння кінцевою обчислювальною схемою й називається погрішністю апроксимації. Крім цього в загальному балансі відіграють роль погрішності, що виникають на кожному кроці інтегрування в результаті використання наближеного значення 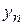 замість точного
замість точного 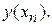 Їх звичайно відносять до погрішностей обумовленим неточностями в завданні вихідних даних і розглядають окремо.
Їх звичайно відносять до погрішностей обумовленим неточностями в завданні вихідних даних і розглядають окремо.
Методи Рунге-Кутта. Розглянемо рівняння (1). Інтегруючи його на проміжку 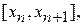 одержимо
одержимо
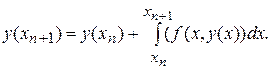
Тоді після заміни 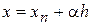 , де
, де 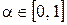 , для приросту на n-ом кроці одержимо вираження
, для приросту на n-ом кроці одержимо вираження
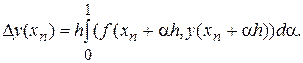 (10)
(10)
Таким чином, задача обчислення значення функції 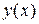 в крапці
в крапці 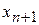 зводиться до обчислення інтеграла в співвідношенні (10). Однак використання традиційних квадратурних формул для цих цілей проблематично, тому що значення
зводиться до обчислення інтеграла в співвідношенні (10). Однак використання традиційних квадратурних формул для цих цілей проблематично, тому що значення 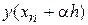 невідомі. У методах Рунге - Кутта квадратурні схеми будуються в такий спосіб.
невідомі. У методах Рунге - Кутта квадратурні схеми будуються в такий спосіб.
Уводяться три групи параметрів 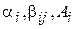 , де
, де
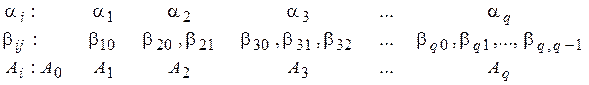 ,
,
якими розпоряджаються так. Перша група параметрів визначає набір вузлових значень 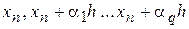 по першої змінної подинтегральной функції
по першої змінної подинтегральной функції 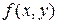 . Друга група параметрів визначає набір вузлових значень по еї другий змінної. Причому виробляється це непрямим образом через прирости
. Друга група параметрів визначає набір вузлових значень по еї другий змінної. Причому виробляється це непрямим образом через прирости 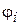 функції
функції 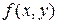 в попередніх вузлових крапках, де
в попередніх вузлових крапках, де
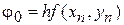 ,
,
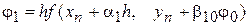 ,
,
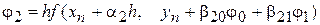 ,
,
........
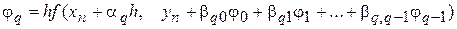 .
.
Нарешті, третя група параметрів 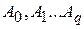 використовується для формування квадратурної формули
використовується для формування квадратурної формули
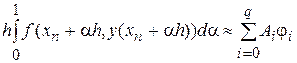 .
.
Таким чином, остаточно
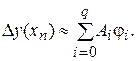 (11)
(11)
Позначимо погрішність співвідношення (11) через 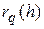 , тобто
, тобто
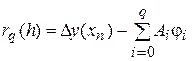
або
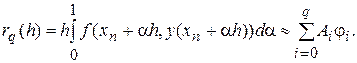
Представимо її за допомогою формули Тейлора у вигляді розкладання по ступенях h
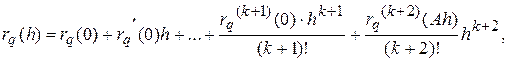
де 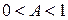 .
.
Якщо зажадати тепер, щоб 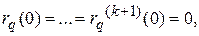 одержимо погрішність співвідношення (11) рівну
одержимо погрішність співвідношення (11) рівну 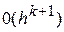 й, отже, погрішність методу рівну
й, отже, погрішність методу рівну 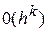 .
.
До числа найбільш уживаних ставляться методи 4-го порядки точності. Для них значення 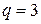 . Один з варіантів відповідного набору параметрів наступний
. Один з варіантів відповідного набору параметрів наступний
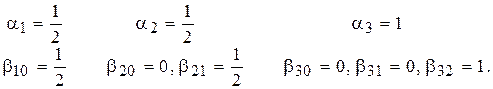
Тоді вираження 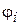 мають вигляд
мають вигляд
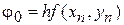 ,
,
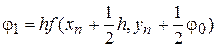 ,
,
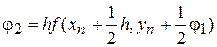 ,
,
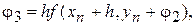
коефіцієнти 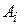 ,-
,-
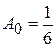 ,
, 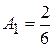 ,
, 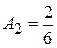 ,
, 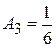
і обчислювальне правило, у цілому,
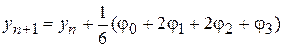 .
.
На Малюнку 2 у смузі 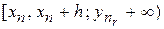 зазначені використовувані в цьому методі вузлові крапки. Значення
зазначені використовувані в цьому методі вузлові крапки. Значення 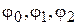 обрані довільно.
обрані довільно.
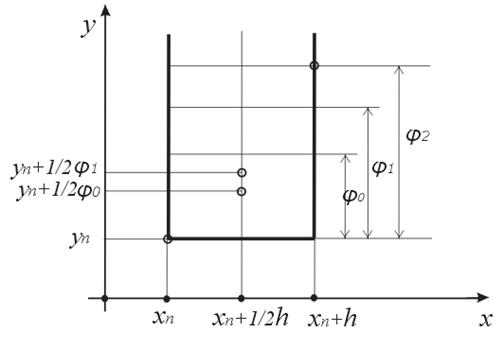
Малюнок 2. Вузлові крапки методу Рунге-Кутта 4-го порядку
Правило Рунге. Для оцінки погрішності чисельних результатів інтегрування при використанні однокрокових методів на практиці звичайно застосовують правило Рунге, що полягає в наступному.
Теоретично показано, що головний член погрішності апроксимації має вигляд 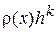 , де k – порядок методу,
, де k – порядок методу, 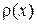 - деяка функція, обумовлена особливостями правої частини диференціального рівняння.
- деяка функція, обумовлена особливостями правої частини диференціального рівняння.
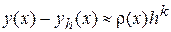 ,
,
де 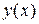 , - точне значення,
, - точне значення, 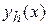 , наближене, певне при проведенні розрахунків із кроком h. Тоді, проводячи розрахунки із кроком
, наближене, певне при проведенні розрахунків із кроком h. Тоді, проводячи розрахунки із кроком 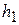 і
і 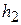 , одержуємо
, одержуємо
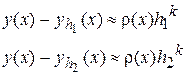 .
.
Дозволяючи, далі, наближену систему цих співвідношень відносно 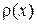 , маємо
, маємо
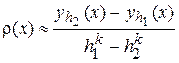 ,
,
звідки
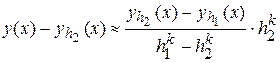 . (12)
. (12)
Співвідношення (12) і представляє правило Рунге. Природно, воно дає достовірні результати лише в тому випадку, що коли домінує в загальній погрішності результату є погрішність методу.
Звичайно правило (12) використовують при 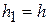 ,
, 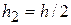 . Тоді
. Тоді
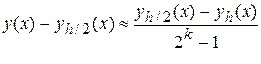 .
.
Зокрема, для методів Эйлера (k=1)
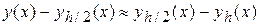 ,
,
методу трапецій (k =2), -
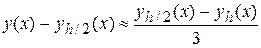 ,
,
методу Рунге – Кутта четвертого порядку (k =4),-
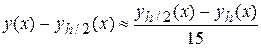 .
.
 2015-08-21
2015-08-21 453
453








