2015-08-21
363
Нагадаємо основні положення теорії рядів Фур'є.
Нехай є деяка функція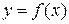 
, задана на проміжку 
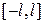й розглядається нескінченна система функцій
.
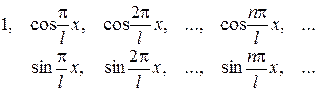Ставиться задача про подання даної функції у вигляді тригонометричного ряду
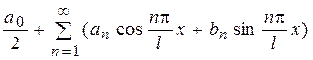(1)
Таке подання за певних умов можливо і його коефіцієнти обчислюються по наступних формулах
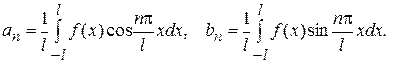(2)
Тригонометричний ряд (1) з коефіцієнтами (2) називається поруч Фур'є функції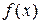 
.
Справедлива наступна теорема про розкладність (т. Дирихле):
Якщо 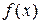кусочно-монотонна функція й має не більш, ніж кінцеве число крапок розриву першого роду, то її ряд Фур'є (1), (2) сходиться до значення 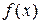в крапках її безперервності й до середнього арифметичного її однобічних меж у крапках розриву.
Так, наприклад, якщо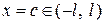 
крапка розриву 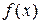, то сума ряду Фур'є в цій крапці дорівнює
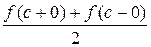- (Малюнок 1),
де
, 
.
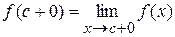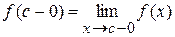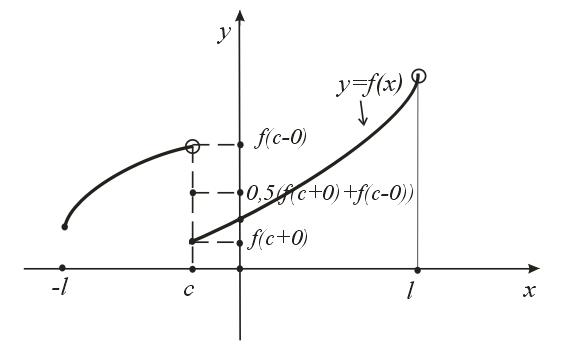
Малюнок 1. Пояснення до теореми Дирихле
Т.о. за винятком, бути може, кінцевого числа крапок сума ряду Фур'є (1), (2) дорівнює .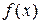
Зауваження 1. У крапках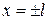 
ряд Фур'є сходиться до середньої арифметичної правої й лівої меж функції 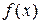в крапках 
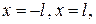відповідно.
Оборотний увага на особливості розкладання в ряд Фур'є парних і непарних функцій.
Якщо 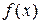парна на відрізку 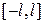, те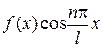 
, також парна, а 
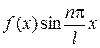, - непарна. Тому коефіцієнти
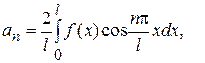
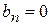
і розкладання (1) приймає вид
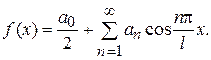
Якщо ж функція 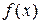непарна, то 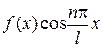також непарна, а 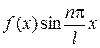, - парна.
Тому
, 
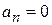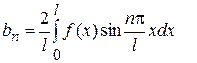
і розкладання (1) приймає вид
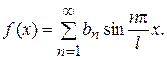
Зауваження 2. Вираження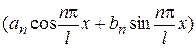 
в розкладанні (1), уводячи допоміжний кут, можна представити у вигляді 
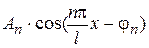, де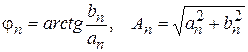 
й ряд у цілому
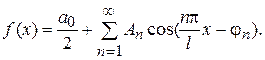
Тоді доданки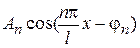 
називаються гармонійними складовими або гармоніками, коефіцієнти 
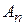- амплітудами гармонік, 
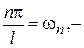частотами, 
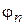- початковими фазами. Іноді гармоніка 
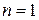називається основний, гармоніки 
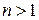, - побічними.
Зауваження 3. Іноді тригонометричні розкладання заданої функції будуються на проміжку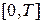 
. У цьому випадку розглядається система тригонометричних функцій
1,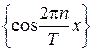 
, 
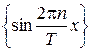
і розкладання має вигляд
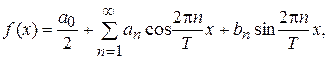(3)
де
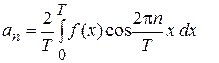(4)
.
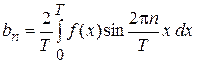Теорема Дирихле для проміжку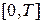 
формулюється відповідно аналогічним образом.
