Третья итерация

6)Найдем f_min=min{-2,169;-4,5;-1,3877}=-4,5 => x_min=3

7)Вычислим точку минимума полинома, построенного по 3-м точкам:

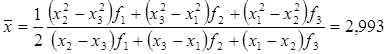
f(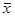)=-4,4869

8)Проверим выполнение условий окончания:

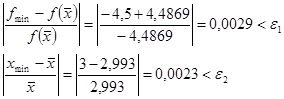Так как условия выполнены, следовательно поиск закончен.

Решение: х*≈ 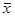=2,993 точка минимума; f(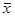)=-4,4869

Релакционная последовательность:

xk			3,3	2,549	2,7	3,1	2,9	2,939	2,993
f(xk)			32,227	22,675	10,904	-1,3877	-2,169	-3,581	-4,4869	-4,5

Алгоритм равномерного поиска

Шаг 1. Задать начальный интервал неопределенности 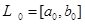, N – количество вычислений функции.

Шаг 2. Вычислить точки 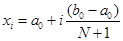, , равноотстоящие друг от друга.

Шаг 3. Вычислить значения функции в N найденных точках: .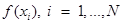

Шаг 4. Среди точек 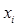() найти такую, в которой функция принимает наименьшее значение .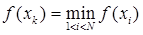

Шаг 5. Точка минимума 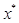принадлежит интервалу L_N = [ x_{k -1}, x_{k+ 1}], на котором в качестве приближённого решения может быть выбрана точка .

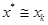Алгоритм метода дихотомии

Шаг 1. Задать начальный интервал неопределенности 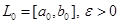– малое число, 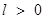– точность.

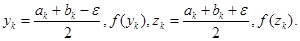Шаг 2. Положить .

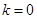Шаг 3. Вычислить

Шаг 4. Сравнить 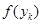с :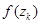

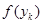
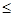
а) если 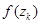, положить 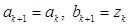(рис. 5.6, а) и перейти к
шагу 5;

б) если 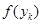> 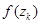), положить 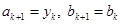(рис. 5.6, б).

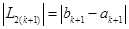Шаг 5. Вычислить и проверить условие окончания:

а) если 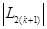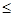l, процесс поиска завершается и 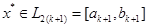. В качестве приближенного решения можно взять середину последнего интервала:

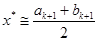
б) если 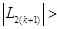l, положить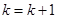 и перейти к шагу 3.

Для метода дихотомии характеристика относительного уменьшения начального интервала неопределенности находится по формул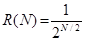е , где
N – количество вычислений функции.

Алгоритм квадратичной интерполяции

Шаг 1. Задать начальную точку х ₁, величину шага 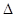х > 0, 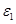и 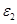– малые положительные числа, характеризующие точность.

Шаг 2. Вычислить .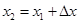

Шаг 3. Вычислить 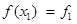и .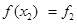

Шаг 4. Сравнить 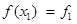c :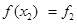

а) если 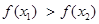, положить 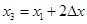(рис. 5.11, а);

б) если 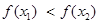, положить 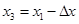(рис. 5.11, б).

Шаг 5. Вычислить .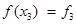

Шаг 6. Найти .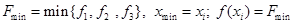

Шаг 7. Вычислить точку минимума интерполяционного полинома, построенного по трем точкам,

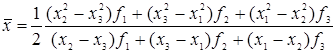
и величину функции 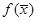(рис. 5.11).

Если знаменатель в формуле для 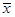на некоторой итерации обращается в нуль, то результатом интерполяции является прямая. В этом случае рекомендуется обозначить 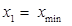и перейти к шагу 2.

Шаг 8. Проверить выполнение условий окончания: .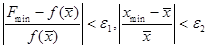

Тогда:

а) если оба условия выполнены, процедура закончена и ;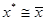

б) если хотя бы одно из условий не выполнено и 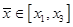, выбрать наилучшую точку ( 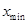или 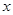) и две точки по обе стороны от неё. Обозначить эти точки в естественном порядке и перейти к шагу 6;

в) если хотя бы одно из условий не выполнено и 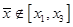, то положить 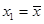и перейти к шагу 2.