Непрерывной СВ X наз. Распределённая по нормальному закону (по закону Гаусса) с параметрами mx и σx, если её плотность распр-я вероятностей определяется выражением:
f(x)= 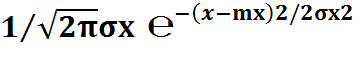
Фун-ция распределения определяется:
F(x)= 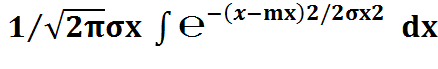

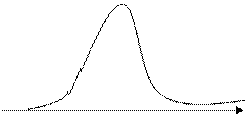
 График плотности распределения наз. нормальной кривой/кривой Гаусса и имеет вид:
График плотности распределения наз. нормальной кривой/кривой Гаусса и имеет вид:
 | ||||
 | ||||
 | ||||
Вероятность попадания СВ в интервал (α,β):
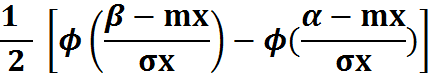
где 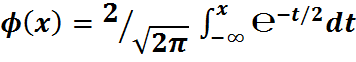 - ф-я Лапласса
- ф-я Лапласса
Следствие: P(|x- mx|<ε)= 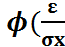 )
)
21.Неравенства Маркова и Чебышева и различные формы их записи. Формулировка нер-ва Маркова Если среди зн СВ Х нет отриц, то вер-ть того, что она примет какое-н зн, превосходящее полож число А, не больше дроби 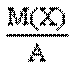 , т.е.
, т.е. 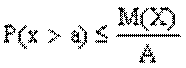 , а вер-ть того, что она примет какое-н зн, не превосходящее полож числа А, не меньше
, а вер-ть того, что она примет какое-н зн, не превосходящее полож числа А, не меньше 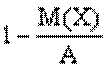 , т.е.
, т.е. 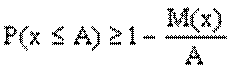 1а я форма нер-ва Чебыш Вер-ть того, что отклонение СВ Х от ее матеможидания, а произойдет по абсолютной величине постоянное число Е>0, не больше
1а я форма нер-ва Чебыш Вер-ть того, что отклонение СВ Х от ее матеможидания, а произойдет по абсолютной величине постоянное число Е>0, не больше 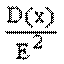 , т.е.
, т.е. 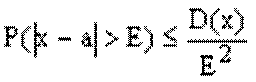 2а я форма нер-ва Чебыш Вер-сть того, что отклонение СВ Х от ее матеможидания, а не произойдет по абсолютной величине постоянного числа Е>0, не меньше
2а я форма нер-ва Чебыш Вер-сть того, что отклонение СВ Х от ее матеможидания, а не произойдет по абсолютной величине постоянного числа Е>0, не меньше 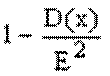 , т.е.
, т.е. 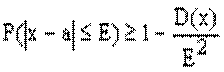 Говорят,что послед-сть СВ
Говорят,что послед-сть СВ 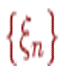 сходится по вер-ти к Св
сходится по вер-ти к Св 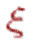 при
при 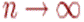 , и пишут
, и пишут 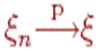 , если для люб
, если для люб 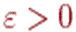

 2015-08-12
2015-08-12 539
539








