Структурная схема лабораторной установки

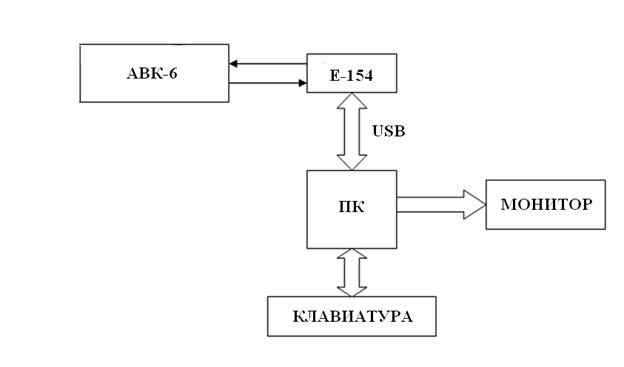
АВК-6 – аналоговый вычислительный комплекс.

Е-154 – измерительный модуль.

ПК – персональный компьютер.

Модель формирования сигнала

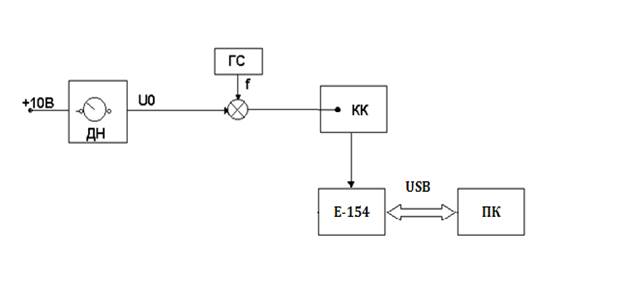
ДН – делитель напряжения, ГС – генератор сигналов, КК – клеммная колодка, Е-154 – измерительный модуль, ПК – персональный компьютер.

Задание:

Экспериментальное исследование свойств и особенностей следующих алгоритмов первичной обработки информации:

· фильтрации;

· проверки достоверности информации;

· аналитической градуировки датчика;

Разностные уравнения исследуемых алгоритмов:

- Разностные уравнения фильтров экспоненциального сглаживания и скользящего среднего:

В непрерывном варианте свойства фильтра экспоненциального сглаживания описывается дифференциальным уравнением:

.

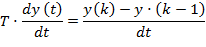
Передаточная функция звена описывается уравнением:

.

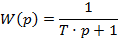
Дифференциальное уравнение апериодического звена имеет вид:

.

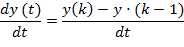
Заменив производную разностью, получено разностное уравнение:

_,

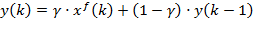где γ – параметр настройки фильтра, вычисляемый по формуле:

,

,

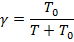
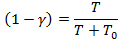
где Т – постоянная времени, Т₀ – период опроса датчика.

В аналоговом виде (непрерывный вариант) уравнение фильтра скользящего среднего имеет вид:

.

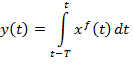
Заменив интеграл суммой (применяя для интегрирования метод прямоугольников), получено:

,

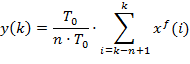
где Т – время усреднения, вычисляемое по формуле:

,

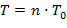
где n – число точек усреднения, параметр настроек фильтра.

- Разностные уравнения статистических фильтров:

Передаточная функция статистического фильтра первого порядка описывается уравнением:

.

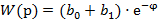
Математическое ожидание описывается уравнением:

.

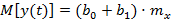
Несмещенная оценка фильтра описывается уравнением:

.

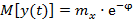
При учете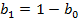

,

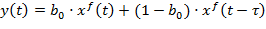где 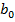, 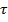- параметры настройки фильтра.

Минимизируя значение ошибки фильтрации, получено:

.

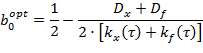
Для программной реализации 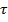берут равную T₀ – период опроса датчика.

Разностное уравнение:

.

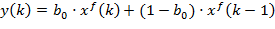При n =0 имеем статистический фильтр нулевого порядка W (p)= b₀

.

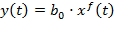При использовании данной формулы y (t) будет смещённой оценкой полезного сигнала x (t), т.е.

,

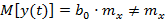где 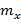-математическое ожидание выходного сигнала.

Для получения несмещённой оценки необходимо использовать следующую функцию:

.

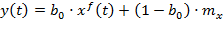В этом случае математическое ожидание описывается уравнением:

,

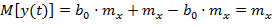где b₀ – параметр настройки, описывается уравнением:

.

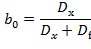
Для программной реализации статистического фильтра нулевого порядка используют формулу:

.

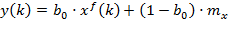Асимптотические полиномы:

Достоинствомявляетсявозможность предварительной оценки степени полинома до расчёта коэффициента. Расчёт коэффициентов асимптотических полиномов приведен в таблице: