Орієнтація двосторонньої незамкнутої поверхні: вибирається певна сторона поверхні  ; на кожній замкнутій кривій на
; на кожній замкнутій кривій на  визначається додатний напрям обходу так, що він разом з нормаллю вибраної сторони утворював праву трійку векторів.
визначається додатний напрям обходу так, що він разом з нормаллю вибраної сторони утворював праву трійку векторів.
Нехай в точках поверхні  , розташованої однозначно над площиною
, розташованої однозначно над площиною 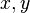 і заданою явно рівнянням
і заданою явно рівнянням 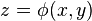 , визначена обмежена функцією
, визначена обмежена функцією 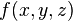 . Нехай
. Нехай 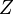 є розбиття поверхні
є розбиття поверхні  на скінченну кількість елементарних поверхонь
на скінченну кількість елементарних поверхонь 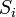 ,
, 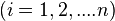 ,
, 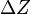 — найбільший діаметр елементарних поверхонь,
— найбільший діаметр елементарних поверхонь, 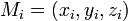 — довільна точка, вибрана на елементарній поверхні
— довільна точка, вибрана на елементарній поверхні 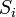 . Якщо вибрана певна сторона поверхні і тим самим орієнтація по ній, то напрям обходу межі кожної елементарної поверхні
. Якщо вибрана певна сторона поверхні і тим самим орієнтація по ній, то напрям обходу межі кожної елементарної поверхні 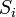 визначає напрям обходу в площині
визначає напрям обходу в площині 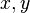 , біля кордону проекції
, біля кордону проекції 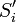 . Площа
. Площа 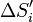 цієї проекції береться із знаком «+», якщо межа проекції
цієї проекції береться із знаком «+», якщо межа проекції 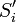 проходиться в додатному напрямі; інакше — із знаком «—» (Рис. 2).
проходиться в додатному напрямі; інакше — із знаком «—» (Рис. 2).
Число
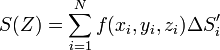
називається інтегральною сумою, що відповідає розбиттю 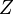 . На противагу утворенню інтегральних сум поверхневих інтегралів 1-го роду, тут
. На противагу утворенню інтегральних сум поверхневих інтегралів 1-го роду, тут 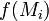 множиться не на площу
множиться не на площу 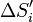 (елементарній поверхні
(елементарній поверхні 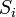 а на взяту із знаком площа
а на взяту із знаком площа 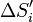 проекції
проекції 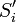 поверхні
поверхні 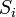 на площину
на площину 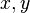 .
.
Якщо існує число 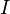 з такою властивістю: для кожного
з такою властивістю: для кожного 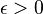 знайдеться таке
знайдеться таке 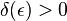 , що для кожного розбиття
, що для кожного розбиття 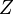 з
з 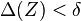 , незалежно від вибору точок
, незалежно від вибору точок 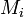 , завжди |
, завжди | 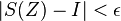 , то
, то 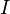 називають поверхневим інтегралом 2-го роду від
називають поверхневим інтегралом 2-го роду від
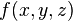 за вибраною стороною
за вибраною стороною  і пишуть
і пишуть
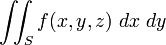
Якщо  не має взаємно однозначної проекції на площину
не має взаємно однозначної проекції на площину 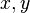 , але її можна розбити на скінченну кількість поверхонь, для кожної з яких існує така проекція, то поверхневий інтеграл по
, але її можна розбити на скінченну кількість поверхонь, для кожної з яких існує така проекція, то поверхневий інтеграл по  визначається як сума інтегралів по окремих поверхнях.
визначається як сума інтегралів по окремих поверхнях.
Якщо  має однозначну проекцію на площину
має однозначну проекцію на площину 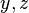 або
або 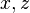 , то можна визначити аналогічно два інших поверхневих інтеграла 2-го роду
, то можна визначити аналогічно два інших поверхневих інтеграла 2-го роду
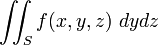
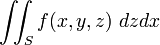
де у відповідних інтегральних сумах стоять площі проекцій 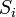 на площину
на площину 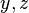 або
або 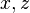 .
.
Нарешті, для трьох функцій 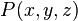 ,
, 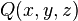 ,
, 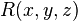 , визначених на
, визначених на  , ці інтеграли можна додати і визначити загальніший поверхневий інтеграл другого роду:
, ці інтеграли можна додати і визначити загальніший поверхневий інтеграл другого роду:
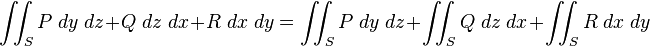
 2015-08-13
2015-08-13 1147
1147








