Скаля́рне по́ле — у векторному численні скалярна функція просторових координат. Скалярне поле ставить певне числове значення, дійсне або комплексне, у відповідність кожній точці простору.
Основною диференціальною операцією над скалярним полем у векторному численні є градієнт.
Скалярними полями описуються фізичні поля, які не залежать від орієнтації системи координат.
Означення. Якщо в кожній точці області V задана скалярна величина 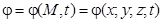 , то кажуть, що на множині V задане скалярне поле
, то кажуть, що на множині V задане скалярне поле 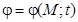 .
.
Означення. Поле називається стаціонарним, якщо функція 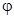 не залежить від часу t, тобто
не залежить від часу t, тобто 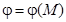 .
.
Для наочного зображення скалярного поля 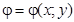 використовують лінії рівня:
використовують лінії рівня:
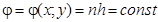 , тут h – крок, n =1,2…...
, тут h – крок, n =1,2…...
Ве́кторне по́ле — Означення. Якщо в кожній точці області V заданий вектор 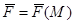 , то кажуть, що в області V задане векторне поле.
, то кажуть, що в області V задане векторне поле.
Векторне поле 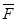 називається потенційним, або безвихровим, якщо для
називається потенційним, або безвихровим, якщо для 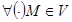
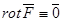 .
.
Векторне поле 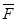 називається соленоїдальним, або трубчастим, якщо для
називається соленоїдальним, або трубчастим, якщо для 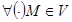
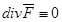 .
.
Векторне поле 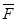 називається гармонійним, якщо воно потенційне й соленоїдальне одночасно, тобто
називається гармонійним, якщо воно потенційне й соленоїдальне одночасно, тобто 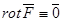 ,
, 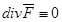 .
.
Коли початковий простір — евклідовий (скінченновимірний векторний простір зі скалярним добутком), поняття векторного поля стає наочним, і тоді векторне поле інтерпретується як спосіб завдання рухів деякої динамічної системи: вектор у даній точці описує напрям і швидкість руху точки по фазовій кривій.
Якщо вибрати декартову систему координат, то поле може бути подане як:
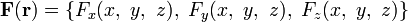
Математичні операції над векторними полями вивчають у векторному аналізі.
Серед характеристик векторного поля 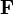 відрізняють диференційні, що стосуються поведінки поля в окремих точках (дивергенція
відрізняють диференційні, що стосуються поведінки поля в окремих точках (дивергенція 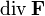 і ротор
і ротор 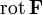 ), та інтегральні, що описують поле вздовж контура (циркуляція) або крізь певну поверхню (потік).
), та інтегральні, що описують поле вздовж контура (циркуляція) або крізь певну поверхню (потік).
Диференційні й інтегральні характеристики векторного поля пов'язані між собою теоремами Гауса,Остроградського та Стокса.
Для поля механічного походження, дивергенція й потік характеризують наявність джерел і стоків у полі, а ротор і циркуляція — обертальну здатність поля.
Чимало фізичних явищ описують за допомогою векторних полів. Наведемо такі приклади:
· Електричне поле;
· Магнітне поле;
· Поле швидкостей потоку рідини чи газу в гідродинаміці.
Похідна вектор-функції:
Означення. Якщо існує границя 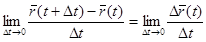 , то вона називається похідною вектор-функції й позначається
, то вона називається похідною вектор-функції й позначається 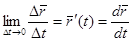 .
.
Наслідок. Оскільки 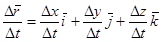 , то з існування
, то з існування 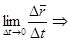 існування границь
існування границь 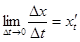 ,
, 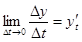 ,
, 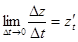 і навпаки.
і навпаки.
Таким чином для того, щоб 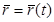 мала похідну, необхідно й достатньо, щоб
мала похідну, необхідно й достатньо, щоб 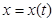 ,
, 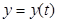 ,
, 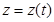 були диференційовані.
були диференційовані.
 2015-08-13
2015-08-13 3299
3299







