1. Нехай поверхня  має явне представлення
має явне представлення 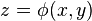 , причому
, причому 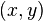 змінюються в області
змінюються в області 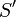 . Тоді поверхневий інтеграл по тій стороні
. Тоді поверхневий інтеграл по тій стороні  , для якої кут між нормаллю і віссю
, для якої кут між нормаллю і віссю 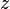 є гострим, обчислюється так:
є гострим, обчислюється так:
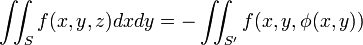
Якщо вибрана інша сторона поверхні, то
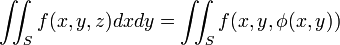
Аналогічні формули виходять для інших інтегралів:
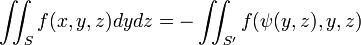
де  задана рівнянням
задана рівнянням 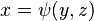 ,
, 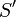 — проекція
— проекція  на площину
на площину 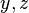 , а поверхневий інтеграл береться по тій стороні, нормаль до якої утворює з віссю
, а поверхневий інтеграл береться по тій стороні, нормаль до якої утворює з віссю 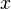 гострий кут. Так само
гострий кут. Так само
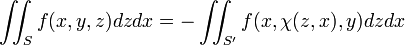
де  задана рівнянням
задана рівнянням 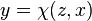 ,
, 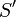 проекція
проекція  на площину
на площину 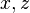 , а поверхневий інтеграл береться по тій стороні, нормаль до якої складає з віссю у гострий кут.
, а поверхневий інтеграл береться по тій стороні, нормаль до якої складає з віссю у гострий кут.
2. Якщо поверхня  задана в параметричній формі:
задана в параметричній формі: 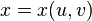 ,
, 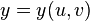 ,
, 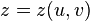 , то
, то
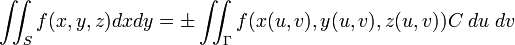
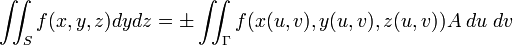
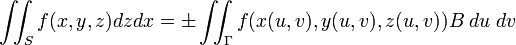
де
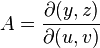
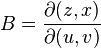
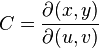
дивись рівняння угорі, додатний знак перед інтегралом справа використовується тоді, коли орієнтація області 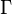 площини
площини 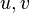 відповідає орієнтації вибраної сторони. Для суми трьох інтегралів отримуємо
відповідає орієнтації вибраної сторони. Для суми трьох інтегралів отримуємо
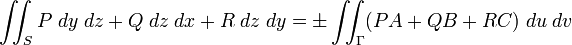
 2015-08-13
2015-08-13 497
497








