Якщо 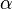 ,
, 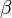 ,
, 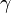 — кути нормалі до вибраної сторони поверхні з осями
— кути нормалі до вибраної сторони поверхні з осями 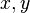 і
і 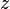 , то
, то
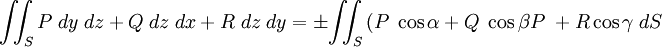
тобто поверхневий інтеграл 2-го роду, що стоїть зліва, перетвориться в поверхневий інтеграл 1-го роду, що стоїть справа.
Поверхневий інтеграл
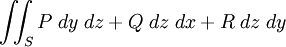
має для різних незамкнутих поверхонь 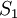 і
і 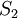 з однією і тією ж границею
з однією і тією ж границею 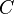 у загальному випадку різні значення (Рис. 3), тобто він в загальному випадку не обертається в нуль на замкнутій поверхні (аналогічно залежності від шляху криволінійного інтеграла). Якщо функції
у загальному випадку різні значення (Рис. 3), тобто він в загальному випадку не обертається в нуль на замкнутій поверхні (аналогічно залежності від шляху криволінійного інтеграла). Якщо функції
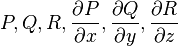
неперервні в однозв'язній просторовій області 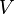 (тобто в області, яка разом з кожною замкнутою поверхнею містить також і область, обмежену цією поверхнею), то поверхневий інтеграл по всякій замкнутій поверхні
(тобто в області, яка разом з кожною замкнутою поверхнею містить також і область, обмежену цією поверхнею), то поверхневий інтеграл по всякій замкнутій поверхні  в
в 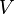 обертається в нуль тоді і тільки тоді, коли
обертається в нуль тоді і тільки тоді, коли
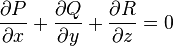
 2015-08-13
2015-08-13 364
364








