Нехай деяка функція 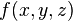 визначена і обмежена на гладкій поверхні
визначена і обмежена на гладкій поверхні  . Хай
. Хай 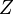 позначає деяке розбиття
позначає деяке розбиття  на скінченну кількість елементарних поверхонь
на скінченну кількість елементарних поверхонь 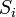 (i = 1, 2 …. і) з площами
(i = 1, 2 …. і) з площами 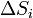 ,
, 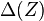 є найбільшим діаметром елементарних поверхонь
є найбільшим діаметром елементарних поверхонь 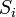 і
і 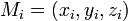 — довільна точка на відповідній елементарній поверхні (Рис. 1). Число
— довільна точка на відповідній елементарній поверхні (Рис. 1). Число
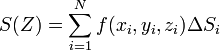
називається інтегральною сумою, що відповідає розбиттю 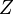 . Якщо існує число
. Якщо існує число 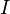 з такою властивістю: для кожного
з такою властивістю: для кожного 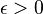 знайдеться таке
знайдеться таке 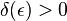 , що для кожного розбиття
, що для кожного розбиття 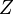 з
з 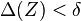 , незалежно від вибору точок
, незалежно від вибору точок 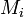
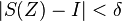 , то
, то 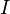 називається поверхневим інтегралом 1-го роду від
називається поверхневим інтегралом 1-го роду від 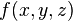 по поверхні
по поверхні  і записується
і записується
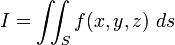
Для окремого випадку підінтегрального виразу 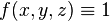
число 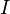 дає площу
дає площу  поверхні
поверхні  .
.
Обчислення (зведення до подвійного інтеграла): якщо поверхня задана параметрично:
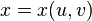 ,
, 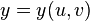 ,
, 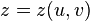 ,
,
причому 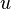 та
та 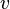 пробігають область
пробігають область 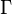 площини
площини 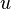 ,
, 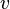
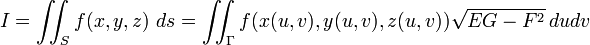
Якщо поверхня задана явно рівнянням 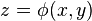 причому
причому 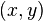 пробігають область
пробігають область 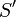 , то
, то
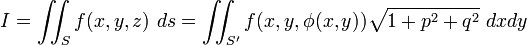
Аналогічні формули вірні, якщо  представлена рівняннями виду
представлена рівняннями виду 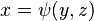 чи
чи 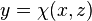
 2015-08-13
2015-08-13 310
310








