3 сұрақ
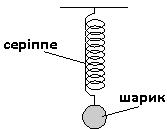
3.1 суретте қатаңдығы k серіппеге ілінген массасы m шарик көрсетілген.
[Сурет 3.1]
(а) Шарикті ілгендегі серіппенің созылу ұзындығын e анықтаңыз.
| e = | [1] |
(b) Шарикті үлкен қашықтыққа А (A<e) тартып, жібереді. Шарик тігінен жоғары-төмен тербеледі.
(i) Шарик тербелістің төменгі тепе теңдік жағдайында болғандағы қорытқы күштің бағыты мен шамасын анықтаңыз.
| Күштің бағыты= | ||||
| Күштің шамасы= | [1] | |||
(ii) Келесі теңдеуге бағынатын тербелісті сипаттаңыз:
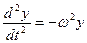
| 1. | [1] |
| 2. | [1] |
| 3. | [1] |
| Барлығы: | [3] |
(iii) Тербелістегі шариктің максималды жылдамдығын анықтайтын теңдеуді жазыңыз.
| максималды жылдамдық = | [1] |
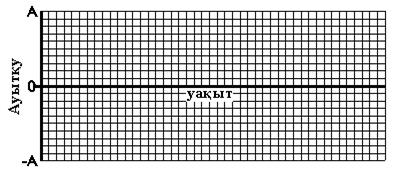
(c) Шариктің ауытқуы тепе теңдік нүктесіне қатысты өлшенеді. 3.2 суретке шариктің ауытқуының уақытқа тәуелділік графигін салыңыз. Уақыт шарикті босатқан сәттен басталады.
[Сурет 3.2]
(d) Шарикті жібергенде, оның тепе теңдікке алғаш рет оралғандағы энергия өзгерісін сипаттаңыз.
| [2] |
(e) Массасы 0,24 кг шарик қатаңдығы 1,5 Н/м серіппеге ілініп, тік бағытта ығыстырылады.
Шариктің тербелу периодың анықтаңыз.
| период = | [2] |
[Барлығы: 10]
| 3-сұрақ | Жауап | Балл | ||
| (a) | (e =) mg / k | |||
| (b) | (i) | Күштің бағыты = Жоғары Күштің шамасы = kA-mg | ||
| (ii) | - Үдеу - күшке қарама-қарсы бағытталған және теріс мәнге ие. - үдеу = (–) ky / m - ω 2 = k / m | максимум 3 | ||
| (iii) | (максималды жылдамдық =) Aω немесе A √(k / m) | |||
| (c) | - дұрыс периодтың синусоидты қисығының графигі - дұрыс синусоидты период және Aω немесе A √(k / m) остеріндегі дұрыс қисықтың графигі | максимум 2 | ||
| (d) | - серіппенің потенциалдық энергиясынан - кинетикалық және потенциалдық (гравитациялық) энергияға | максимум 2 | ||
| (e) | -(период =)2π/ω немесе2π/√(k / m) немесе 2π√(m / k) немесе2π/√(1.5/0.24) немесе2π√(0.24/1.5) немесе 2π/√6.25 немесе 2π√ 0.16немесе2π/2.5 немесе 2π0.4, π=3.142 - 2.51 с | максимум 2 | ||
| [Барлығы: 12] | ||||
 2015-08-13
2015-08-13 394
394








