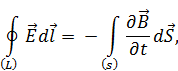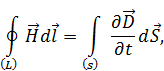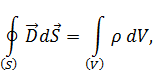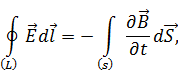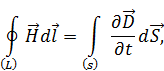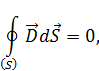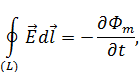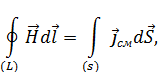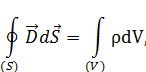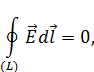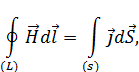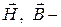 магнитные вектора,
магнитные вектора, 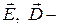 электрические вектора.
электрические вектора.
Стационарные поля – 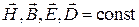 , т. е. не зависят от времени. В правой части уравнений Максвелла нет производных по времени
, т. е. не зависят от времени. В правой части уравнений Максвелла нет производных по времени 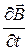 или
или 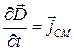 . Нестационарные (переменные) поля –
. Нестационарные (переменные) поля – 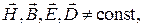 т. е. зависят от времени. В правой части уравнений Максвелла есть указанные выше производные.
т. е. зависят от времени. В правой части уравнений Максвелла есть указанные выше производные.
Если есть нестационарное магнитное поле, значит есть и нестационарное электрическое и наоборот. Если нет нестационарного магнитного поля, значит нет и нестационарного электрического и наоборот, так как они взаимосвязаны.
Есть два источника электрического поля: для стационарного – только неподвижные заряды, для нестационарного (переменного) – движущиеся заряды и нестационарное (переменное) магнитное поле.
Есть два источника магнитного поля: для стационарного – только постоянные токи проводимости, для нестационарного (переменного) – переменные токи проводимости и нестационарное (переменное) электрическое поле («токи» смещения).
Магнитное поле – всегда вихревое, так как 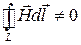 . Электрическое поле может быть потенциальным, когда
. Электрическое поле может быть потенциальным, когда 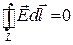 и вихревым, когда
и вихревым, когда 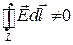 .
.
1. 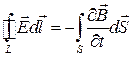 или
или 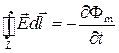 ,
,
так как Фm 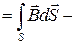 магнитный потоки поэтому
магнитный потоки поэтому 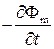
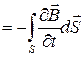 .
.
– источником вихревого электрического поля (слева вектор 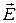 ) является нестационарное магнитное поле (справа производная по времени
) является нестационарное магнитное поле (справа производная по времени 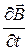 ),
),
– уравнение электромагнитной индукции Фарадея,
2. 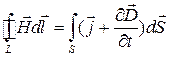 или
или 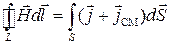 или
или 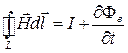 ,
,
так как 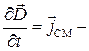 векторплотности «тока» смещения,
векторплотности «тока» смещения, 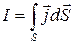 плотность тока проводимости,Фe
плотность тока проводимости,Фe 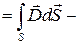 электрический потоки поэтому
электрический потоки поэтому 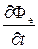
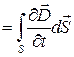 .
.
– источником вихревого магнитного поля (слева вектор 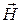 ) являются токи проводимости (справа
) являются токи проводимости (справа 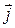 ) и нестационарное электрическое поле (справа производная по времени
) и нестационарное электрическое поле (справа производная по времени 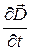 ),
),
3. 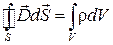 или
или 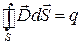 илиФe = q,
илиФe = q,
так как 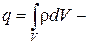 свободныйэлектрическийзаряд; заряженное тело.
свободныйэлектрическийзаряд; заряженное тело.
– источником потенциального электрического поля (слева вектор 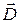 ) являются электрические заряды (справа
) являются электрические заряды (справа 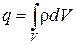 ),
),
– теорема Остроградского – Гаусса для электрического поля в среде.
4. 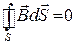 .
.
– отсутствие магнитных зарядов,
– теорема Остроградского – Гаусса для магнитного поля.
Любое скалярное произведение векторов имеет вид:
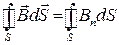 ,
, 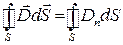 ,
, 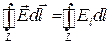 ,
, 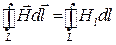 .
.
Для простоты исключим нулевые решения и будем считать, что если в правой части уравнений Максвелла есть выражения, то они не равны нулю. Тогда возможны следующие варианты систем уравнений.
1. Нет в правой части 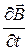 и
и 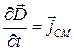 – следовательно, нет нестационарных полей, т. е. заряды неподвижны, а токи постоянны. В результате есть только стационарные электрические и магнитные поля. (
– следовательно, нет нестационарных полей, т. е. заряды неподвижны, а токи постоянны. В результате есть только стационарные электрические и магнитные поля. (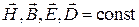 ).
).
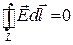 ,
, 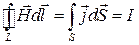 ,
, 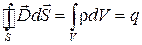 ,
, 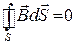 .
.
В этом случае электрические и магнитные поля независимы друг от друга.
2. Нет в правой части 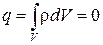 – следовательно, нет стационарного электрического поля, а есть нестационарное электрическое и в общем случае оба магнитных поля. В результате есть электромагнитное поле в отсутствии свободных зарядов или при наличии токов проводимости и в отсутствии (свободных) зарядов и заряженных тел.
– следовательно, нет стационарного электрического поля, а есть нестационарное электрическое и в общем случае оба магнитных поля. В результате есть электромагнитное поле в отсутствии свободных зарядов или при наличии токов проводимости и в отсутствии (свободных) зарядов и заряженных тел.
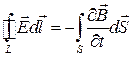 ,
, 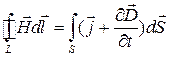 ,
, 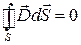 ,
, 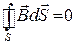 .
.
3. Нет в правой части 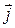 (
(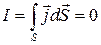 ) – следовательно, нет стационарного магнитного поля, а есть нестационарное магнитное и в общем случае оба электрических поля. В результате есть электромагнитное поле в отсутствии токов проводимости или при наличии (свободных) зарядов и заряженных тел и в отсутствии токов проводимости.
) – следовательно, нет стационарного магнитного поля, а есть нестационарное магнитное и в общем случае оба электрических поля. В результате есть электромагнитное поле в отсутствии токов проводимости или при наличии (свободных) зарядов и заряженных тел и в отсутствии токов проводимости.
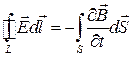 ,
, 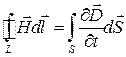 ,
, 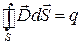 ,
, 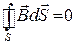 .
.
4. Нет в правой части 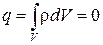 и
и 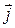 (
(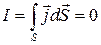 ) – следовательно, нет стационарных электрических и магнитных полей, а есть только нестационарные электрические и магнитные поля. В результате есть электромагнитное поле в отсутствие токов проводимости и (свободных) зарядов и заряженных тел, (частный случай – электромагнитные волны.)
) – следовательно, нет стационарных электрических и магнитных полей, а есть только нестационарные электрические и магнитные поля. В результате есть электромагнитное поле в отсутствие токов проводимости и (свободных) зарядов и заряженных тел, (частный случай – электромагнитные волны.)
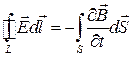 ,
, 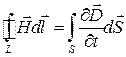 ,
, 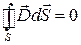 ,
, 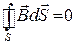 .
.
5. Нет в правой части 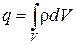 ,
, 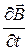 и
и 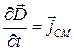 – следовательно, нет электрических полей и нестационарных магнитных. В результате есть только стационарное магнитное поле (
– следовательно, нет электрических полей и нестационарных магнитных. В результате есть только стационарное магнитное поле (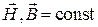 ).
).
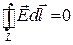 ,
, 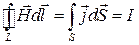 ,
, 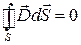 ,
, 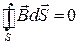 .
.
6. Нет в правой части 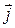 ,
, 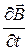 и
и 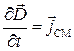 – следовательно, нет магнитных полей и нестационарных электрических. В результате есть только стационарное электрическое поле (
– следовательно, нет магнитных полей и нестационарных электрических. В результате есть только стационарное электрическое поле (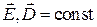 ).
).
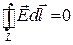 ,
, 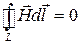 ,
, 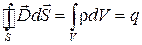 ,
, 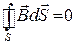 .
.
|
1. Полная система уравнений
Максвелла для электромагнитного
поля в интегральной форме имеет вид: 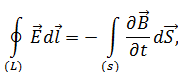 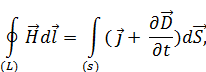 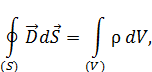 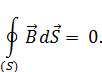 – электромагнитного поля при наличии заряженных тел и в отсутствие токов проводимости, – электромагнитного поля в отсутствие заряженных тел и токов проводимости, – стационарных электрических и магнитных полей, – электромагнитного поля при наличии заряженных тел и токов проводимости. – электромагнитного поля при наличии заряженных тел и в отсутствие токов проводимости, – электромагнитного поля в отсутствие заряженных тел и токов проводимости, – стационарных электрических и магнитных полей, – электромагнитного поля при наличии заряженных тел и токов проводимости. |
|
Максвелла для электромагнитного
поля в интегральной форме имеет вид:
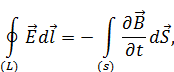 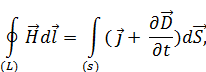 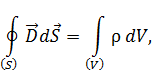 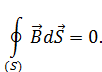 – электромагнитного поля в отсутствие свободных зарядов и токов проводимости, – электромагнитного поля в отсутствие свободных зарядов и токов проводимости, | ||
| – электромагнитного поля в отсутствие свободных зарядов, | ||
| – электромагнитного поля в отсутствие токов проводимости, | ||
– стационарных электрических и магнитных полей.
|
3. Полная система уравнений
Максвелла для электромагнитного
поля в интегральной форме имеет вид: 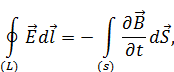 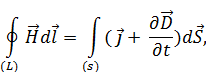 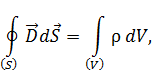 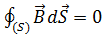 . – электромагнитного поля при наличии заряженных тел и в отсутствие токов проводимости, – электромагнитного поля в отсутствие заряженных тел и токов проводимости, – стационарных электрических и магнитных полей, – электромагнитного поля при наличии заряженных тел и токов проводимости. . – электромагнитного поля при наличии заряженных тел и в отсутствие токов проводимости, – электромагнитного поля в отсутствие заряженных тел и токов проводимости, – стационарных электрических и магнитных полей, – электромагнитного поля при наличии заряженных тел и токов проводимости. |
|
4. Полная система уравнений
Максвелла для электромагнитного
поля имеет вид:
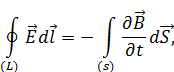
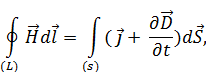
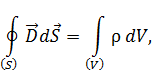
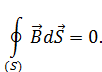
– стационарного электромагнитного поля в отсутствие заряженных тел,
– стационарных электрических и магнитных полей,
– стационарного электромагнитного поля в отсутствие токов проводимости,
– переменного электромагнитного поля при наличии заряженных тел и токов проводимости.
5. Обобщением теоремы Остроградского – Гаусса для электростатического поля в среде является уравнение …
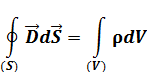
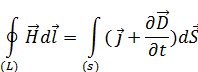
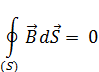
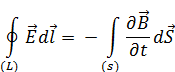
 2015-08-13
2015-08-13 5908
5908