Нами уже рассмотрен закон полного тока (Ампера):
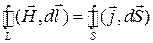 ,
,
полученный в результате большого количества экспериментов. Тем не менее, он не точно отображает закон природы и вступает в противоречие с опытом, если ток не постоянен по времени. Чтобы это показать, рассмотрим экспериментальную установку (рисунок 30).

Рисунок 31 − К определению понятия тока смещения
На этом рисунке изображен конденсатор, обкладки которого начинают заряжаться после включения рубильника. Для проверки выражения полного тока окружим мысленно левую обкладку конденсатора замкнутой поверхностью. При этом поверхность будет проходить в воздухе между обкладками конденсатора и будет пересекать проводник, подводящий ток к левой обкладке. В выражении полного тока можно также перейти к замкнутой поверхности 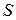 . Для этого надо представить себе поверхность, почти замкнутую, с малым отверстием, по границе которого проведен контур
. Для этого надо представить себе поверхность, почти замкнутую, с малым отверстием, по границе которого проведен контур  . Так как выражение годно для любой поверхности, то оно сохранит свою силу и в этом случае. Затем контур будем мысленно стягивать в точку. Поскольку сила магнитного поля не может быть бесконечно большой, так как в этом случае запас энергии в данном месте был бы бесконечным, то при стремлении контура к нулю будет стремиться к нулю и циркуляция магнитного поля по этому бесконечно малому контуру, то есть левая часть выражения обратится в нуль:
. Так как выражение годно для любой поверхности, то оно сохранит свою силу и в этом случае. Затем контур будем мысленно стягивать в точку. Поскольку сила магнитного поля не может быть бесконечно большой, так как в этом случае запас энергии в данном месте был бы бесконечным, то при стремлении контура к нулю будет стремиться к нулю и циркуляция магнитного поля по этому бесконечно малому контуру, то есть левая часть выражения обратится в нуль: 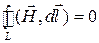 . Следовательно, и правая часть будет равна нулю:
. Следовательно, и правая часть будет равна нулю: 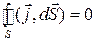 . Между тем, конденсатор заряжается через проводник, перерезанный этой замкнутой поверхностью. Это противоречит выражению.
. Между тем, конденсатор заряжается через проводник, перерезанный этой замкнутой поверхностью. Это противоречит выражению.
Чтобы избежать указанного противоречия, Максвелл дополнил выражение током смещения, который зависит от вектора электрической индукции 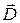 . Этот вектор зависит от силы электрического поля
. Этот вектор зависит от силы электрического поля  и от свойств среды. Наиболее проста эта зависимость в вакууме, для которого
и от свойств среды. Наиболее проста эта зависимость в вакууме, для которого

где 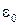 − постоянная величина. В других средах коэффициент пропорциональности между вектором электрического поля и вектором электрической индукции может и не быть постоянной величиной, а направления в пространстве векторов поля и индукции могут и не совпадать.
− постоянная величина. В других средах коэффициент пропорциональности между вектором электрического поля и вектором электрической индукции может и не быть постоянной величиной, а направления в пространстве векторов поля и индукции могут и не совпадать.
Выражение закона полного тока в исправленном Максвеллом виде содержит слагаемое, прибавляющееся к вектору плотности тока, связанного с переносом зарядов, и записывается так:
 .
.
Величину 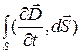 Максвелл назвал током смещения. Ток смещения, получается за счет интегрирования вектора плотности тока смещения
Максвелл назвал током смещения. Ток смещения, получается за счет интегрирования вектора плотности тока смещения
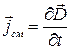 .
.
Полный ток
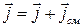 .
.
Ток смещения ликвидирует отмеченное противоречие между опытом и законом полного тока в домаксвелловской формулировке. При заряде конденсатора между его обкладками появляется электрическое поле, а вместе с ним появляется и вектор электрической индукции, и так как электрическая индукция растет, то ее производная по времени положительна, и появляется ток смещения. Так как (применяя то же рассуждение, которое мы применили ранее к замкнутой поверхности) ток смещения и ток проводимости должны в сумме дать нуль через любую замкнутую поверхность, то ток проводимости, текущий по проводнику в обкладку конденсатора, должен быть в точности равен току смещения, «вытекающему» через поверхность. Слово «вытекающий» здесь применяется по аналогии с током, вызванным перемещением зарядов. На самом деле ток смещения никуда не течет подобно магнитному потоку.
Описанное обобщение закона полного тока называется первым уравнением Максвелла в интегральной форме. В литературе его приводят в двух формах:
 ,
,
или, что то же самое
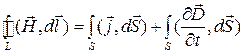 .
.
Для перехода к дифференциальной форме уравнения применим теорему Стокса:
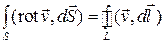
Применяя ее к левой части первого уравнения Максвелла в интегральной форме, получим:
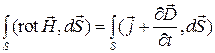
Так как поверхность 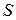 произвольна, то это равенство возможно только при равенстве подынтегральных выражений, т.е.
произвольна, то это равенство возможно только при равенстве подынтегральных выражений, т.е.
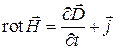 ,
,
что называется дифференциальной формой первого уравнения Максвелла. Это уравнение связывает между собой векторы магнитного поля, электрической индукции и плотности тока в точке пространства.
Все векторные уравнения Максвелла есть краткая запись трех скалярных уравнений, которые немедленно получаются, как только выбрана определенная система координат, и векторы, входящие в уравнения, спроектированы на соответствующие орты в произвольной точке пространства. Тогда возникают, как принято говорить «уравнения Максвелла в координатной форме». Самым простым и распространенным является использование декартовых координат. Обращаясь к основным положениям векторного анализа и раскрывая операцию ротора, первое уравнение можно записать в виде:
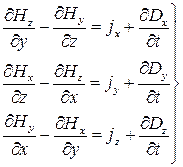
 2015-10-22
2015-10-22 1172
1172
