2015-08-13
353
Сложение и вычитание двух комплексных чисел определяются таким способом:
то есть надо сложить (или вычесть) отдельно вещественные и мнимые части чисел:
.
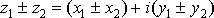Умножение.
Умножение двух комплексных чисел производится как умножение обычных чисел, надо лишь помнить, что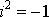 
:
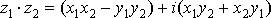
Деление.
Для деления комплексных чисел полезно запомнить следующее правило: чтобы разделить два комплексных числа друг на друга надо числитель и знаменатель умножить на число, комплексно сопряженное знаменателю. Тогда легко получить, что
.
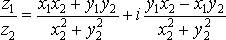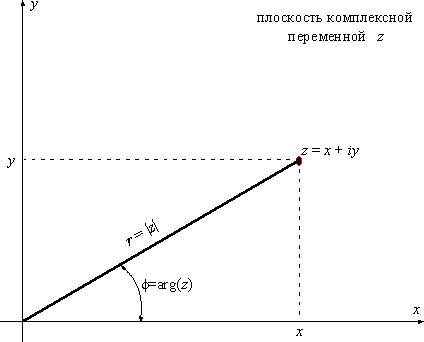
9) Пусть имеется комплексное число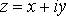 
. Возьмем на плоскости декартову систему координат и комплексному числу z поставим в соответствие точку на этой плоскости с координатами (x, y). Таким образом, геометрически комплексные числа – это точки на плоскости. Саму плоскость называют плоскостью комплексной переменной z.
10) Нера́венство треуго́льника - это одно из свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Неравенство треугольника включается как аксиома в определение нормы(нормированного пространства).
Пусть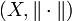 
- нормированное векторное пространство, где X — произвольное множество, а 
— определённая на X норма. Тогда по определению последней справедливо:
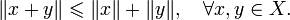
Нормированным векторным пространством называется пара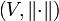 
, где V — векторное пространство, а 
норма в V.
