2015-08-21
289
У воднеподiбному атомi навколо ядра з зарядом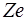 
(
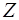- порядковий номер хiмiчного елементу) рухається тiльки один електрон. Потенцiйна енергiя взаємодiї його з ядром дорiвнює:
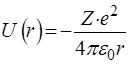. (76)
На рисунку 8 показано криву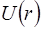 
. З нього видно, що водневоподiбний атом можна розглядати як своєрiдну потенцiйну яму, обмежену потенцiйною кривою. Електрон у цiй ямi володiє негативною енергiєю.
Пiдставляючи (76) у (14), одержимо рiвняння Шредiнгера, яке описує стацiонарний стан водневоподiбного атому:
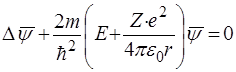. (77)
Рис. 8. Залежнiсть енергiї взаємодiї електрону з ядром
воднеподiбного атома вiд вiдстанi.
Рiшення цього рiвняння дає наступні основні результати.
1. Електрон у водневоподiбному атомi володiє дискретним енергетичним спектром. Власнi значення енергiї визначаються формулою:
, (78)
де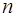 
- головне квантове число.
На рисунку 8 показане розташування енергетичних рiвнiв у водневоподiбному атомi.
2. Орбiтальний момент кiлькостi руху електрона може приймати лише наступний ряд дискретних значень:
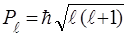, (79)
де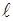 
- орбiтальне (азимутальне) квантове число.
Воно може приймати будь-які значення з наступного цiлочисельного ряду:
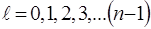(80)
- усього 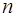значень.
3. Стан з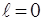 
(при будь-якому 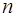) прийнято називати 
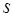-станом, 
- 
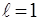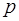-станом, 
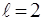- d -станом, 
- 
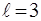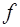-станом і т.д.
4. Орбiтальний момент кiлькостi руху може орiєнтуватися вiдносно вибраного напрямку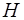 
лише таким чином, що проекцiя його на цей напрямок цiлократна 
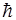(рис. 9):
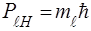. (81)
Число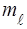 
зветься магнiтним квантовим числом. Воно може приймати усi цiлочисельнi значення вiд 
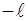до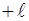 
, включаючи нуль:
(82)
- усього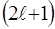 
значень.
Рис. 9. Орiєнтацiя орбiтального моменту кiлькостi руху вiдносно обраного напрямку Н.
