Метод частей

Метод основан на свойствах 6, 7 и позволяет дать двухсторон­ние оценки сопротивлений. Для этого используются вписанные или описанные тела, для которых известно значение сопротивле­ния растеканию. В простейшем случае такими телами могут быть электроды сферической (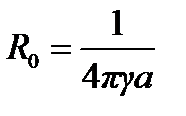) или дисковой формы ().

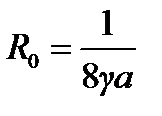Пример 4.3. Оценим сопротивление растеканию уединённого электрода в форме куба с ребром а (рис. 4.20). Для этого впишем и опишем вокруг куба две сферы, так, чтобы одна из них радиу­сом r, целиком принадлежала кубу, а вторая радиусом r₂ цели­ком содержала бы в себе рассматриваемый куб.

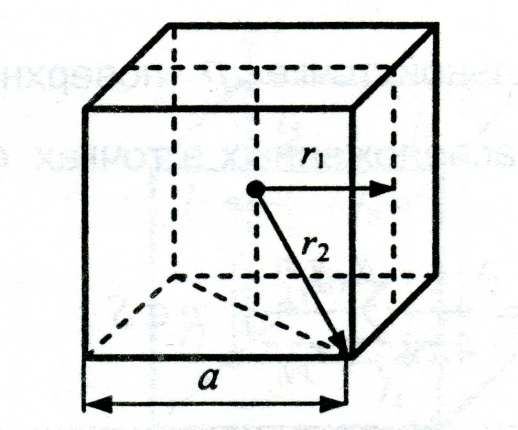
Рис. 4.20. Уединённый электрод в форме куба

Тогда в соответствие со свойством 6 для значения сопротив­ления растеканию рассматриваемого куба R₀ получим оценки вида

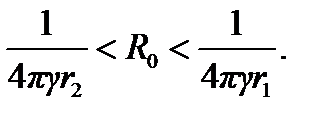
Выражая r₁ и r₂ через а, получим:

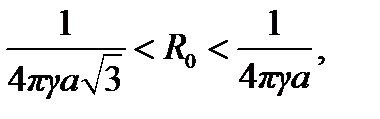или 0.0919 < R₀γa < 0.1592.

Пример 4.4. Дадим двухсторонние оценки электрода в форме квадратной пластины со стороной а. Для этого используем зна­чение сопротивления вписанного и описанного дискового элек­трода (рис. 4.21).

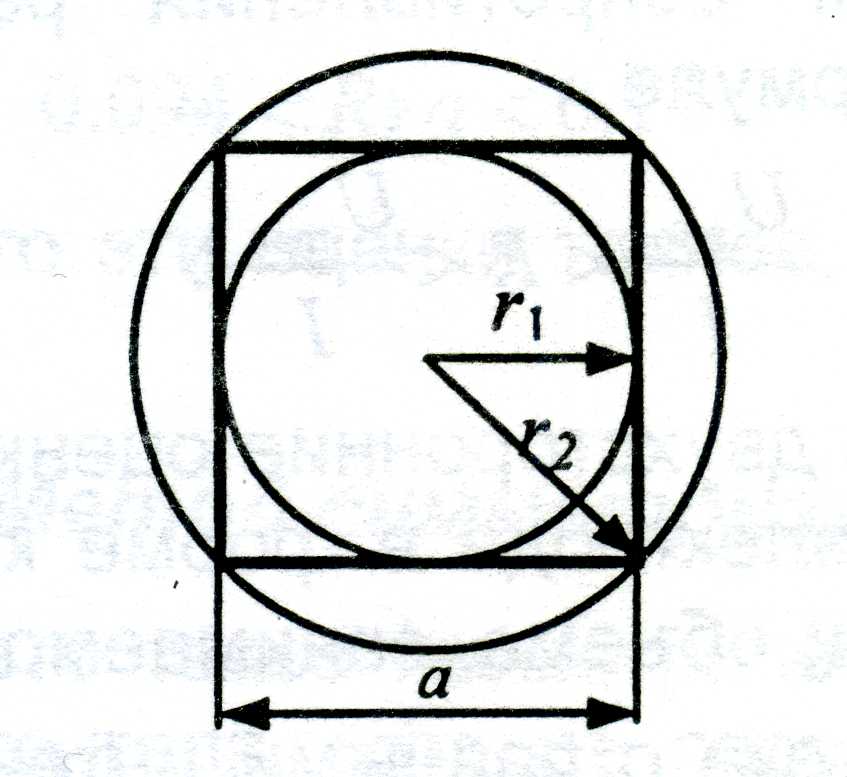
Рис. 4.21 Вписанная и описанная окружности

Учитывая, что r₁ = а /2, а r₂ = 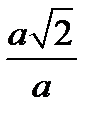, получим 0.1768 < R₀γa < 0.25.