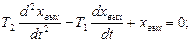
Разделим уравнение на коэффициент, стоящий перед старшей производной:
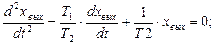
Принимаем: 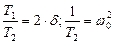 ;
;
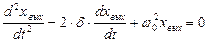
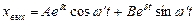
Динамические свойства консервативного звена.
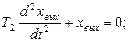
Разделим уравнение на коэффициент, стоящий перед старшей производной: S©
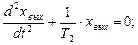
Принимаем: 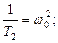
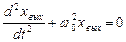 ;
;
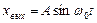 ;
;
Продифференцируем уравнение 2 раза по времени.
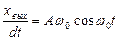 ;
;
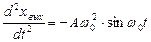 ;
;
После подстановки получаем:
Уравнение 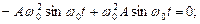 должно быть выполнено, тогда дифференцированное уравнение- частное решение.
должно быть выполнено, тогда дифференцированное уравнение- частное решение.
Таким образом общее решение д.у. 2-го порядка:
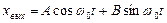 ;
;
Решением д.у. является функция, а не корни!
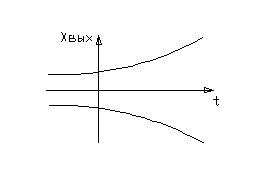
Такая система склонна к незатухающим колебаниям с периодом, который определяется параметрами системы 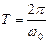 .
.
 2015-08-21
2015-08-21 197
197








