10)
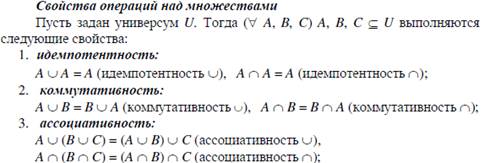

11)Множество M с двумя введенными бинарными операциями (& V), одной унарной операцией (*) и двумя выделенными элементами называется булевой алгеброй, если выполнены свойства (аксиомы булевой алгебры). Булева алгебра всех подмножеств данного множества.
U = {a1, a2… an)
[U] = N
[P(U)] = 2n
Легко показать, что свойства операций над множествами совпадают со свойствами (аксиомами) булевой алгебры. То есть, множество P(U) с операциями объединения, пересечения и дополнения является булевой алгеброй.
Объединение эквивалентно V, пересечение - &, дополнение - *, пустое множество – 0, а универсальное – I. Все аксиомы булевой алгебры справедливы в операциях над множествами.
12) Если число элементов множества неограниченно, то такое множество называется бесконечным. Любое бесконечное множество имеет счетное подмножество.
13) Множества, между которыми можно установить взаимно-однозначное соответствие, называются равномощными (имеющими одинаковую мощность, эквивалентными). Равномощность множеств обозначается символом "~": А ~ В. Для бесконечных множеств мощность множества может совпадать с мощностью его собственного подмножества. Мощность бесконечного мн-ва не изменится если его объединить с конечным ли счетным мн-вом. Во всяком бесконечном мн-ве есть собственное подмн-во, равномощное самому мн-ву. Мн-во всеех подмн-в всякого счетного мн-ва есть мн-во мощности континуума.
|
|
|
14) все элементы с чётного множества можно перенумеровать, то есть обозначить натуральными числами. Другими словами, счётное множество — это множество, равномощное множеству натуральных чисел. Св-ва счетных множеств: 1) объединение конечного и счетного множеств счетно, 2)объединение двух счетных мн-в счетно, 3) декартово произведение 2 счетных мн-в счетно
15) Конти́нуум в теории множеств — мощность множества всех вещественных чисел. Обозначается строчной латинской буквой c во фрактурном начертании: C. Множество, имеющее мощность континуум, называется континуа́льным множеством. 
16) Иерархия бесконечных мн-в
|B(A)=2N Класс счетных мн-в
|B(N)|=2w Класс мн-в мощности континуума
|B(B(N)))|=22w Класс мн-в мощности континуума 2-го порядка
|B(B(B(N)))|=22*2w Класс мн-в мощности 3-го порядка
17) Гипотеза Кантора Любое бесконечное подмножество континуума является либо счётным, либо континуальным. Другими словами, мощность континуума — наименьшая, превосходящая мощность счетного множества, и «промежуточных» мощностей между счетным множеством и континуумом нет. Мощность беконечных множеств образуют дискретный ряд
Комбинаторика
1)Комбинаторика – раздел дискретной математики, который посвящен решению задач пересчёта и перечисления элементов множества, обладающих заданным набором свойств.
|
|
|
Если требуется найти число элементов, принадлежащих данному множеству и обладающих заданными свойствами, то это задача пересчета. Если необходимо выделить все элементы мн-ва. Удовлетворяющие заданным св-ам, то это задача перечисления.
2) Если из множества предметов выбирается некоторое подмножество, то его называют выборкой. Выборки бывают упорядоченные и неупорядоченные. Выборкой объема 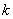 из множества
из множества 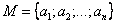 называется всякая последовательность из
называется всякая последовательность из 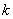 элементов множества
элементов множества 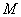 .
.
3) Расположение элементов выборки в определенном порядке называется - упорядочением, при этом выборка называется упорядоченной, в противном случае – неупорядоченной.
4) Правило произведения: пусть имеется n множеств A 1, A 2, …, A n содержащих m 1, m 2, …, m n элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества, т. е. построить кортеж (а1, а2,..., аn), где а i Î А i1 (i = 1, 2, …, n), равно m1 · m2 · … · mn.
5) Теорема «Мощность декартова произведения конечных множеств»
Два конечных множества равномощны тогда и только тогда, когда они состоят из одинакового числа элементов. То есть для конечного множества понятие мощности совпадает с привычным понятием количества.
| А1|=m1…| Аn |=mn
| А1×…×Аn |= m1*...*mn
1)n=1
| А1|=m1
2) Пусть теорема верна при n=k
Докажем для n=k+1
| А1×…×Аk |= m1*...*mk
| А1×…×Аk+1 |= (m1*...*mk )mk+1
6) Правило суммы: пусть имеется n попарно непересекающихся множеств A1, A2, …, An, содержащих m1, m2, …, mn элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно m1 + m2 + … + mn.
7) Мощность объединения множеств. 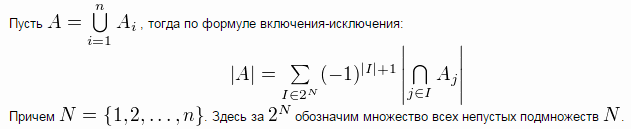
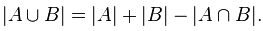
8)Размещения с повторениями и без
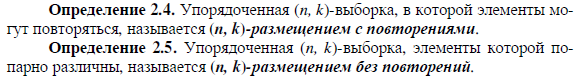
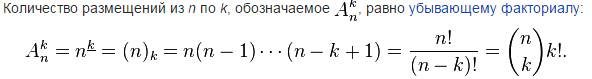

9)Перестановки
Перестановками из n элементов называются соединения, каждое из которых содержит все n элементов, отличающихся поэтому друг от друга только порядком расположения элементов. 
10)Сочетания и их св-ва 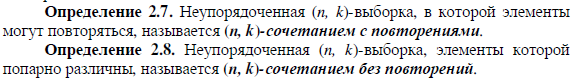
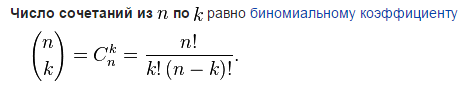
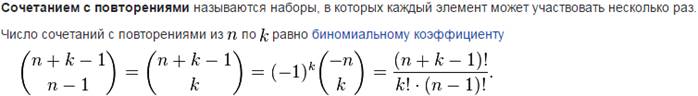
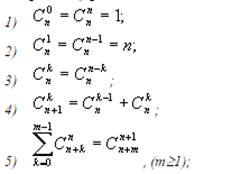
 2015-08-21
2015-08-21 1850
1850







