Обобщенная функция Лагранжа для ЗНП со смешанными ограничениями. Теорема о существовании решения (первая теорема Куна-Таккера)

Рассмотрим задачу нахождения минимума функции цели при смешанных ограничениях.

(*)(этих три строки)

f(x)→min;

g_i(x)=0 (i=1,m)

φ_k(x)≤0;(k=1,5)

Условия регулярности (Слейтера) или условиями смягчающей жесткости называется запись выражения φ_k(x)≤0;(k=1,5) в виде μ_kφ_k(x)=0, причем μ_k – некоторые любые числа и 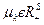(положительному ортанту). Т.е. μ_k≥0. Очевидно что μ_kφ_k(x)=0 в точках на границе области т.к φ_k(x)=0. А в точках внутри области φ_k(x)≤0; то μ_k=0. В этом случае для (*) можно построить обобщенную функцию Лагранжа в виде:

.(**)

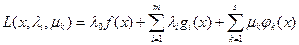Теорема о существовании решения (первая теорема Куна-Таккера).

Если точка х* является точкой локального минимума функции f(x) в области допустимых решений U(x) и g_i(x),φ_i(x)- непрерывны и дифиринцируемые в окрестности точки х*, то существуют такие 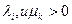одновременно не равные нулю, что для функции Лагранжа (**) выполняются необходимые условия существования экстремума (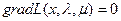) и условие дополнительной нежесткости μ_kφ_k(x)=0.