Теорема. Критерий седловатости точки.
Точка (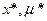 ) при условях (В) есть седловой точкой ф-и Лагранжа тогда и только тогда, когда
) при условях (В) есть седловой точкой ф-и Лагранжа тогда и только тогда, когда
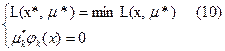
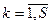
Доказательство:
Необходимости: (следует из определения седл. точки)
По определению седл. точка – это точка минимума.
f (x*)= L(x*,0) < f (x)
из определения: L(x*,0) 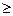 L(x*,
L(x*, 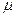 *).
*).
Тогда можем получить что:
f (x*)+ 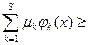 f (x*).
f (x*).
Но в этом случае такого быть не может 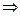 справедливо что
справедливо что 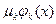 =0
=0 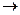 и тогда минимум.
и тогда минимум.
Достаточность:
Пусть (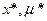 ) есть точка в которой выполняется (10). Тогда следует из (8) что
) есть точка в которой выполняется (10). Тогда следует из (8) что
L(x*, 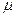 *)= f (x*).
*)= f (x*).
Если это так, то для произвольных 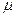 :
:
L(x*, 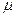 *)= f (x*)
*)= f (x*) 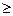 L(x*,
L(x*, 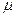 ), и точка (
), и точка (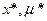 ) – седловая точка.
) – седловая точка.
19. Двойственная функция для ЗНП. Теорема о взаимосвязи экстремумов взаимно двойственных функций.
Двойственная функция в задачах нелинейного програмирования
Пусть 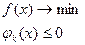
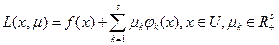
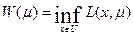 (11)
(11)
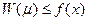 (12) в силу того, что
(12) в силу того, что 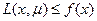
 2015-08-21
2015-08-21 467
467








