Седловая точка обобщенной функции Лагранжа. Теорема Куна-Таккера о Седловой точке

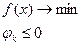
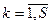(7) L(x, 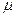)= f (x)+ 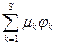(x) (8)

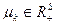
В случа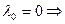е все 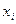какие угодно 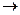не имеет смысла

Точка (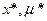), 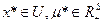(В) называется Седловой точкой ф-и Лагранжа, если:

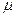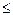L(x*, 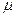) 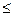L(x*, *) L(x, 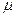*) (9)

Теорема Куна-Такера о Седловой точке L(x)

Если т. (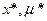) – седловая т. ф-и Лагранжа, удовлетворяющая условию (В), то точка х * есть точкой наименьшего значения ф-и Лагранжа для всех .

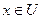Доказательство:

Возьмем произвольное L(x, 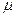). Если 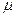< 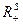, , 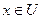то значении ф-и Лагранжа будет

L(x, 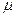) 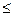f (x) в силу (8), и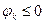

Тогда:

L(x,0) = f (x). Тогда для Седловой точки получим: L(x*,0) 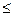f (x*), или просто равно.

Перепишем в виде:

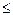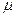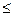f (x*)= L(x*,0) L(x*, *) L(x, 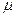*) 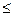f (x).

Тоесть для Седловой точки ф-и Лагранжа значение ф-и цели есть минимум.

Следствие: что бы найти минимум ф-и цели достаточно найти седловую точку ф-и Лагранжа (8).