Обобщенная функция Лагранжа. Теорема о существовании стационарной точки функции Лагранжа

Пусть имеем задачу

Найти 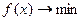(1) при 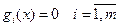(2)

Точки экстремума (1), (2):

1. Точки стационарности
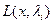
2. Точки, где якобиан =0
3. Точки, в которых хоть одна функция 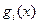не дифференцируема или имеет разрывную частную производную

Когда нужно найти точки при 2) или 3) то для повышения качества вводят дополнительный параметр Лангранжа и строят обобщенную функцию Лангранжа

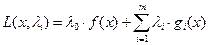(6)

Теорема:

Если точка 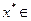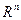- точка условного экстремума функции (1) при условиях (2) причем 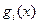- непрерывна в некоторой окрестности 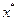и дифференцируемы в этой окрестности то

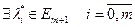причем не все лямбды одновременно равны нулю. Для функции (6) точка 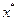есть стационарной, т.е.

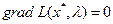
Если 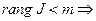линейно независимы и последнее равенство теоремы будет выполнятся когда хоть одно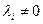

Но положив 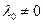запишим

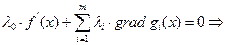получим возможность определить вектор лямбд с точность до нескольких множителей