Найти 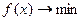 (1) при
(1) при 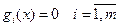 (2) и
(2) и 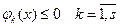 (3)
(3)
Считается что хоть одна из функций в (1),(2),(3) - нелинейная. Считая, что 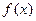 ,
, 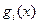 ,
, 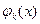 определенные на открытом множестве
определенные на открытом множестве 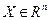
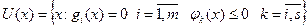
Если 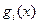 непрерывны то Х замкнуто и совпадает с
непрерывны то Х замкнуто и совпадает с 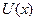
Если по системе ограничений (2), (3) можно сказать, что множество допустимых решений выпукло и функция на этом множестве выпукла то задача минимизации имеет решение, причем каждая точка локального минимума является точкой глобального минимума функции цели.
Теорема:
Если 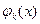
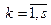 выпуклы в
выпуклы в 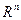 то множество допустимых решений
то множество допустимых решений 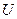 тоже является выпуклым.
тоже является выпуклым.
Доказательство:
Если 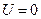 или
или 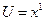 то все катит (очевидно).
то все катит (очевидно).
Если 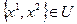
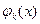 выпукло
выпукло 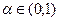 имеем
имеем
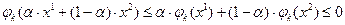
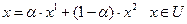
Если область допустимых решений определяется только ограничениями вида (3) и каждая функция 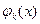 выпукла в
выпукла в 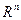 то область допустимых решений также выпукла.
то область допустимых решений также выпукла.
В том случае если присутствуют ограничения типа (2) то доказательство выпуклости усложняется. Однако когда 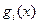 линейны то в этом случае пространство разбивается на подпространства с помощью гиперплоскостей.
линейны то в этом случае пространство разбивается на подпространства с помощью гиперплоскостей.
В этом случае экстремум функции цели будет принадлежать области пересечений ограничений типа (2) и расположенных внутри выпуклой области определенной ограничениями типа (3).
Во многих случаях общую задачу нелинейного программирования можно свести к задаче с ограничениями типа равенств записав (3) в виде
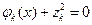
 2015-08-21
2015-08-21 638
638








