Теорема 1 двойственности
Если для некоторых точек 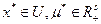 выполняется равенство
выполняется равенство 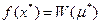 , то функция цели
, то функция цели 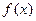 достигает в точке
достигает в точке 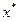 своего наименьшего значения, а функция
своего наименьшего значения, а функция 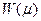 достигает в
достигает в 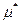 своего наибольшего значения.
своего наибольшего значения.
Доказательство
Из определения функции 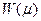 и неравенств (11),(12) вытекает, что
и неравенств (11),(12) вытекает, что 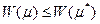
Из (12) следует 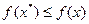 . Следовательно
. Следовательно 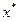 - точка наименьшего значения.
- точка наименьшего значения.
Для выпуклости 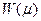 вверх надо показать
вверх надо показать 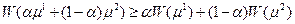
т.к. 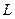 -линейна.
-линейна.
Надо доказать что 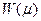 - выпуклая
- выпуклая
Доказательство
Т.к. 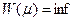 , то
, то 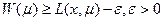 . Получаем, что если взять промежуточную точку
. Получаем, что если взять промежуточную точку 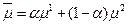 , то
, то 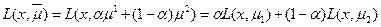
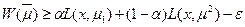
Переходя к определению 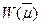
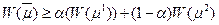
Т.е 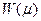 выпукла вверх.
выпукла вверх.
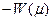 выпукла вниз.
выпукла вниз.
Теорема 2 двойственности
Функция 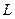 имеет седловую точку тогда и только тогда, когда для
имеет седловую точку тогда и только тогда, когда для 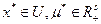
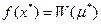
Теоремы двойственности говорят, что для каждой задачи НЛП задачу на минимизацию 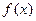 можно заменить на максимизацию двойственной функции
можно заменить на максимизацию двойственной функции 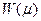 при ограничениях типа неравенств для
при ограничениях типа неравенств для 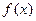 , и
, и 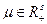 для
для 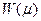 .
.
 2015-08-21
2015-08-21 305
305







