Метод малых возмущений мы будем рассматривать в гидродинамическом приближении Брагинского [2]:
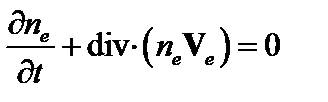 ; (2.1.1)
; (2.1.1)
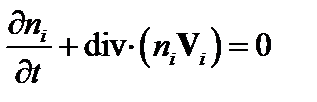 ; (2.1.2)
; (2.1.2)
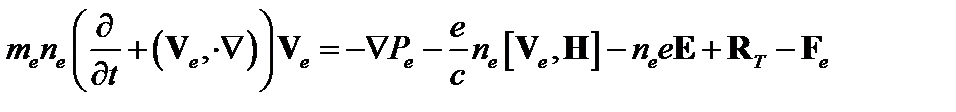 ; (2.1.3)
; (2.1.3)
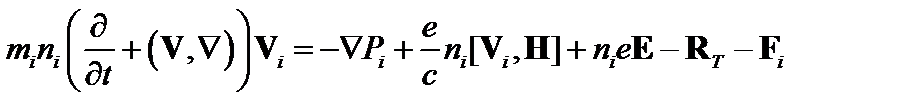 . (2.1.4)
. (2.1.4)
Здесь F e,I – вязкие силы, R – сила трения между электронами и ионами. Остальные обозначения – стандартные.
Будем предполагать квазинейтральность плазмы, то есть 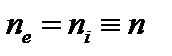 . Ведем массовую скорость
. Ведем массовую скорость
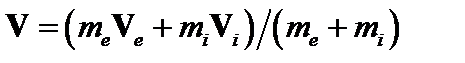 .(2.1.5)
.(2.1.5)
Умножая уравнения (2.1.1) и (2.1.2) на массы электронов и ионов соответственно и суммируя два этих выражения, получаем уравнение непрерывности для плазмы как целого:
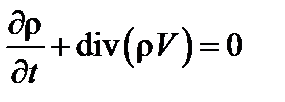 . (2.1.6)
. (2.1.6)
Сложим уравнения (2.1.3) и (2.1.4). Пренебрегая вязкими членами, получаем
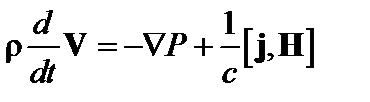 . (2.1.7)
. (2.1.7)
Здесь 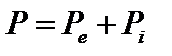 ,
, 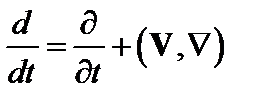 . Во многих задачах инерция электронов пренебрежимо мала. Поэтому положим
. Во многих задачах инерция электронов пренебрежимо мала. Поэтому положим 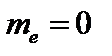 в уравнении (2.1.3). Ток j можно выразить через электронную и ионную скорости:
в уравнении (2.1.3). Ток j можно выразить через электронную и ионную скорости:
J = ne (V i – V e). (2.1.8)
Полагая, что скорость электронов не слишком велика по сравнению со скоростью ионов (это предположение не всегда справедливо), можно положить также 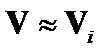 .
.
Для анализа таких гидродинамических неустойчивостей, как винтовая неустойчивость в токамаке, которые развиваются за времена, много меньшие времени между столкновениями, можно пренебречь столкновениями, то есть силами трения между электронами и ионами. В этом случае уравнение (2.1.3) примет вид


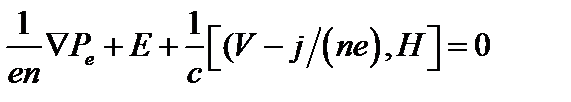 . (2.1.9)
. (2.1.9)
Здесь мы пренебрегли инерцией электронов.
Член [ j, H ] выразим с помощью уравнения (2.1.7).
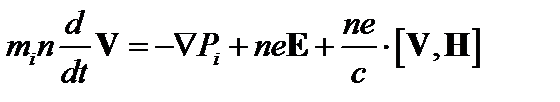 . (2.1.10)
. (2.1.10)
Левую часть уравнения (2.1.10) можно оценить как 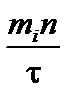 V, где
V, где 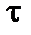 – характерное время развития неустойчивости, а её отношение к последнему члену в правой части – как
– характерное время развития неустойчивости, а её отношение к последнему члену в правой части – как 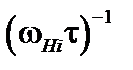 . Здесь
. Здесь 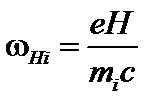 – ионная ларморовская частота. Таким образом, для процессов, характерное время развития которых много больше ионной ларморовской частоты, левую часть уравнения (2.1.10) можно положить равной нулю.
– ионная ларморовская частота. Таким образом, для процессов, характерное время развития которых много больше ионной ларморовской частоты, левую часть уравнения (2.1.10) можно положить равной нулю.
Сравним теперь первый и последний члены в (2.1.10). Для первого члена можно сделать такую оценку:
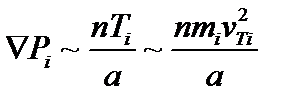 . (2.1.11)
. (2.1.11)
Последний член в правой части (2.1.10)можно оценить следующим образом:
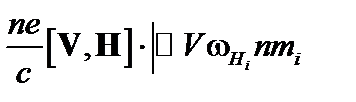 [ V, H ]. (2.1.12)
[ V, H ]. (2.1.12)
Отношение двух этих членов можно представить в виде
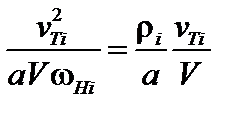 .
.
Здесь 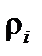 – ионный ларморовский радиус. Если отношение макроскопической скорости плазмы к её тепловой скорости достаточно велико (оставаясь малым по сравнению с единицей),
– ионный ларморовский радиус. Если отношение макроскопической скорости плазмы к её тепловой скорости достаточно велико (оставаясь малым по сравнению с единицей), 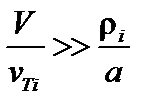 , то в уравнении (2.1.10) можно пренебречь также и градиентом давления. В результате получаем
, то в уравнении (2.1.10) можно пренебречь также и градиентом давления. В результате получаем
E + 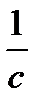 [ V, H ] = 0. (2.1.13)
[ V, H ] = 0. (2.1.13)
В качестве уравнения энергии возьмем адиабату 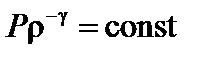 или
или
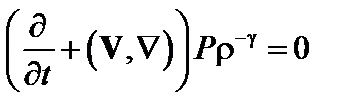 ,
, 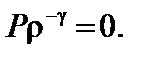 =0. (2.1.14)
=0. (2.1.14)
К материальным уравнениям необходимо добавить уравнения Максвелла:
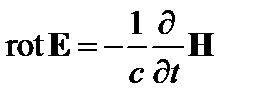 ; (2.1.15)
; (2.1.15)
div H = 0; (2.1.16)
rot H = 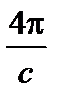 j;(2.1.17)
j;(2.1.17)
В последнем уравнении опущена производная по времени от электрического поля, то есть полученная система уравнений не описывает такие быстрые процессы, как распространение радиоволн в плазме.
Как всегда в методе малых возмущений, ищем все величины в виде суммы, не зависящей от времени невозмущенной величины и малой добавки, H = H 0 + H1; P = P 0+ P 1; 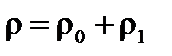 ; E = E1; V = 6. Мы предположили, что невозмущённые значения скорости и электрического поля равны нулю.
; E = E1; V = 6. Мы предположили, что невозмущённые значения скорости и электрического поля равны нулю.
В нулевом приближении получаем
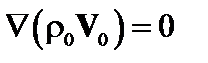 ; (2.1.18)
; (2.1.18)
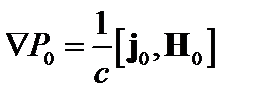 ; (2.1.19)
; (2.1.19)
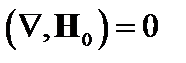 ; (2.1.20)
; (2.1.20)
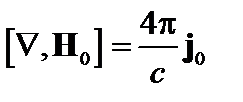 . (2.1.21)
. (2.1.21)
В первом приближении
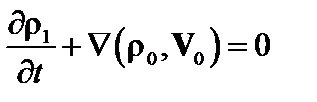 ; (2.1.22)
; (2.1.22)
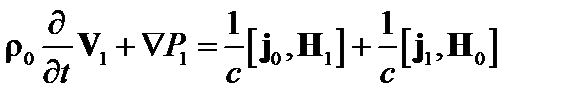 ; (2.1.23)
; (2.1.23)
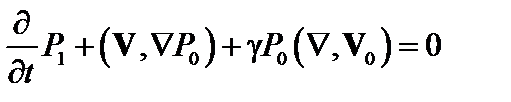 ; (2.1.24)
; (2.1.24)
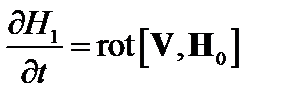 ; (2.1.25)
; (2.1.25)
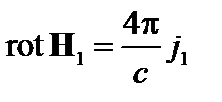 . (2.1.26)
. (2.1.26)
Удобно ввести смещение элемента плазмы 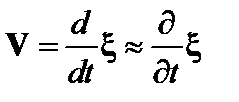 . Последнее равенство получено в первом порядке теории возмущений путем отбрасывания квадратичного по возмущению члена. Уравнение (2.1.25) теперь перепишется следующим образом:
. Последнее равенство получено в первом порядке теории возмущений путем отбрасывания квадратичного по возмущению члена. Уравнение (2.1.25) теперь перепишется следующим образом:
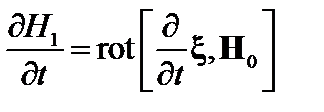 . (2.1.27)
. (2.1.27)
Интегрируя это уравнение по времени, получаем
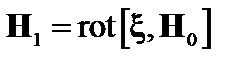 . (2.1.28)
. (2.1.28)
Аналогичным образом получаем
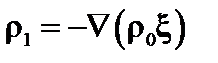 ; (2.1.29)
; (2.1.29)
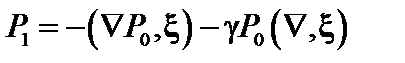 . (2.1.30)
. (2.1.30)
Окончательно, подставляя полученные выражения в уравнение (2.1.23), получаем уравнение второго порядка для 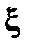
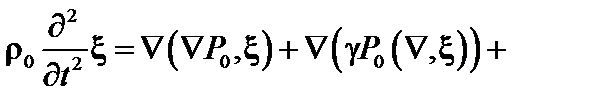
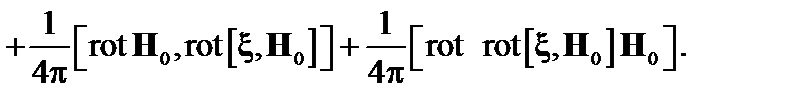 (2.1.31)
(2.1.31)
Уравнение (2.1.31) должно быть дополнено граничными условиями.
Рассмотрим два варианта: на границе плазмы с идеально проводящей стенкой и на границе с вакуумом.
На границе со стенкой смещение плазмы в направлении, перпендикулярном стенке, равно нулю:
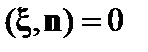 . (2.1.32)
. (2.1.32)
Здесь n – единичный вектор, нормальный к поверхности.
В идеально проводящей плазме составляющая электрического поля, параллельная границе, обращается в ноль:
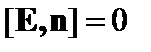 . (2.1.33)
. (2.1.33)
C помощью уравнения (2.1.13) и соотношения V = 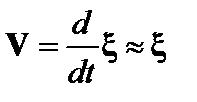 в линейном приближении получаем
в линейном приближении получаем
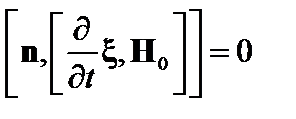 . (2.1.34)
. (2.1.34)
Проинтегрировав (2.1.34) по времени, окончательно получаем граничное условие на бесконечно проводящей неподвижной стенке:
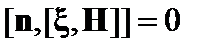 . (2.1.35)
. (2.1.35)
На неподвижной границе «плазма–вакуум» магнитное поле перпендикулярно границе (в противном случае плазма будет вытекать через границу вдоль поля):
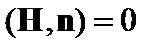 . (2.1.36)
. (2.1.36)
Величины в вакууме и в плазме будем обозначать соответственно индексами «e» (external) и «i» (internal). Равенство полных давлений 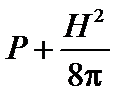 по обе стороны границы раздела имеет вид
по обе стороны границы раздела имеет вид
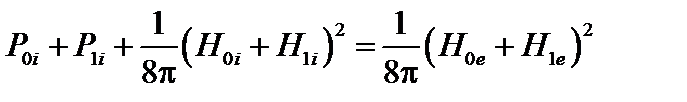 . (2.1.37)
. (2.1.37)
Все величины надо вычислять на смещённой границе 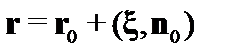 , где индексом «0» обозначены радиус-вектор невозмущенной границы и нормаль к ней. Разлагая в ряд по
, где индексом «0» обозначены радиус-вектор невозмущенной границы и нормаль к ней. Разлагая в ряд по 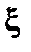 , с учётом (2.1.30), получаем в первом приближении
, с учётом (2.1.30), получаем в первом приближении
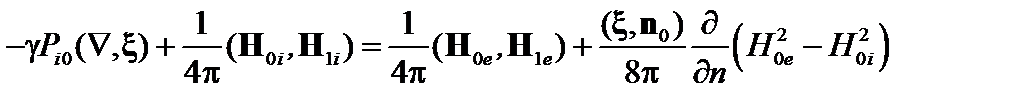 . (2.1.38)
. (2.1.38)
В этом уравнении все значения берутся на невозмущённой границе «плазма–вакуум».
В плазме в системе отсчёта, движущейся вместе с граничной поверхностью, электрическое поле 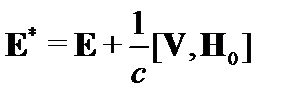 обращается в ноль. Тангенциальная её составляющая
обращается в ноль. Тангенциальная её составляющая 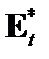 непрерывна. Поэтому
непрерывна. Поэтому
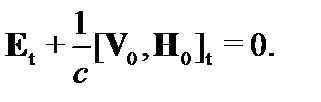 (2.1.39)
(2.1.39)
Так как оба слагаемых в левой части формулы первого порядка малости, их можно взять на невозмущённой границе:
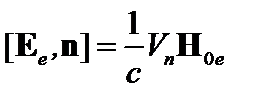 . (2.1.40)
. (2.1.40)
В вакууме электрическое поле выражается через векторный потенциал, 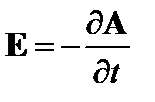 . Выражение (2.1.40) можно переписать в виде
. Выражение (2.1.40) можно переписать в виде
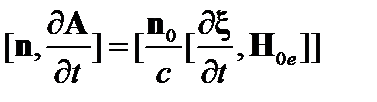 . (2.1.41)
. (2.1.41)
Интегрируя это равенство по времени и учитывая, что магнитное поле параллельно магнитной поверхности, получаем
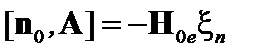 . (2.1.42)
. (2.1.42)
На границе вакуум-стенка смещение обращается в ноль, поэтому 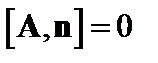 .
.
 2015-08-21
2015-08-21 545
545








